“我并不是说神经网络很容易。 您需要成为该领域专家才能令这些事情发挥作用。 但这些专业知识可助力您跨越广泛的应用边界。 从某种意义上说,以前用于特征设计的所有努力,现在都要投入到架构设计、损失函数设计、以及优化流图设计。 手工劳动已经提升到更高的抽象层次。”
–斯特凡诺·索托(Stefano Soatto)
概述
在上一篇文章中,我们讨论了神经网络的基础知识,并构建了一个非常基本的静态 MLP,但我们知道在现实应用中,我们不需要一个简单的 2 个输入层和 2 个隐藏层节点的网络来输出,有些是我们上次构建的。
有时,与您的问题最相合的网络可能是输入层中有 10 个节点,隐藏层中有 13 个节点/神经元,输出层中有大约四个节点/神经元,更不必提您将不得不微调整个网络中隐藏层的数量。
我的观点是,我们需要一些动态的东西。 一个动态代码,我们可以在不打破程序的情况下更改参数及优化。 如果您使用 python-keras 函数库来构建神经网络,即便架构很复杂,您也能减少配置和编译的工作,这就是我希望我们能够在 MQL5 中达成的目标。
就像我在线性回归 第 3 部分(这是本系列文章中必读的内容之一)中所做的那样,我引入了模型的矩阵/向量形式,从而能够拥有无限输入数量的灵活模型。
矩阵来拯救
我们都知道,当涉及到优化新参数时,硬编码模型会落入钝化,整个过程很耗时,会导致头痛、背部疼痛、等等,(太不值了)。

如果我们抵近观察神经网络背后的操作,您会注意到每个输入都被乘以分配给它的权重,然后它们的输出被添加到乖离之中。 矩阵运算可以很好地处理这一点。
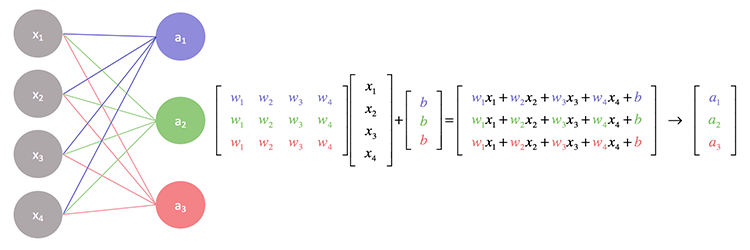
基本上,我们找到输入和权重矩阵的点积,然后最终将其添加到乖离之中。
为了构建一个灵活的神经网络,我将尝试一个奇怪的架构,即输入层中有 2 个节点,第一个隐藏层中有 4 个节点,第二个隐藏层中有 6 个节点,第三个隐藏层中有 1 个节点,最后是输出层中的一个节点。
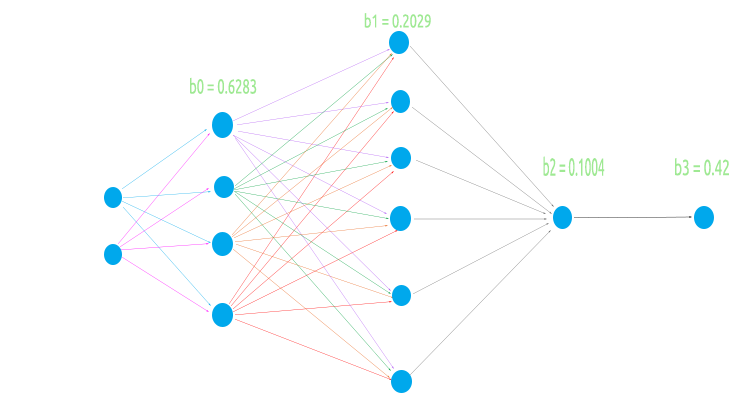
这是为了测试我们的矩阵逻辑在所有情况下是否均都能顺利执行
- 当前一层(输入)的节点数量较少时,下一层(输出层)
- 当前一层(输入)有较多节点时,下一层
- 当输入层和下一层(输出)层中的节点数量相等时
为矩阵运算编写代码,并计算值之前,我们先做一些基本事务,从而令整个运算成为可能。
生成随机权重和乖离值。
//Generate random bias for(int i=0; i<m_hiddenLayers; i++) bias[i] = MathRandom(0,1); //generate weights int sum_weights=0, L_inputs=inputs; double L_weights[]; for (int i=0; i<m_hiddenLayers; i++) { sum_weights += L_inputs * m_hiddenLayerNodes[i]; ArrayResize(Weights,sum_weights); L_inputs = m_hiddenLayerNodes[i]; } for (int j=0; j<sum_weights; j++) Weights[j] = MathRandom(0,1);
我们在上一部分曾看到过这个操作,但需要注意的一点是,这些权重和乖离值应该一次生成,以便运用在世代周期。
什么是世代?
世代是神经网络中所有数据的完整传递,在前馈中是所有输入的完整前向验算,在反向传播中是完整的前向和后向验算。 简而言之,就是神经网络看过所有数据。
与我们在上一篇文章中看到的 MLP 不同,这次我们带来了一个实现,其考虑到输出层中的激活函数,用过 keras 的人可能熟悉这一点,基本上我们可以在隐藏层中拥有不同的激活函数,且其会在输出层引导输出。
CNeuralNets(fx HActivationFx,fx OActivationFx,int &NodesHL[],int outputs=NULL, bool SoftMax=false);
请注意,输入 HActivationFx 是隐藏层中的激活函数,OActivationFx 是输出层中的激活函数,NodesHL[] 是隐藏层中的节点数量。 如果该数组有 3 个元素,这意味着您有 3 个隐藏层,这些层中的节点数量将由数组中存在的元素决定,请参阅下面的代码。
int hlnodes[3] = {4,6,1}; int outputs = 1; neuralnet = new CNeuralNets(SIGMOID,RELU,hlnodes,outputs);
这是我们刚在上面所见图像上的架构。 outputs 参数是可选的,如果将其保留为 NULL,则以下配置将应用于输出层:
if (m_outputLayers == NULL) { if (A_fx == RELU) m_outputLayers = 1; else m_outputLayers = ArraySize(MLPInputs); }
如果您选择 RELU 作为隐藏层的激活函数,则输出层将有一个节点,否则最后一层中的输出数量将等于第一层中的输入数量。 如果您在隐藏层中使用 RELU 以外的其它激活函数,则您有很高机会用到分类神经网络,那么默认输出层将等于列数。 这是不可靠的,尽管输出必须等同于您的数据集中目标特征的数量,如若您尝试解决分类问题,我会在将来的更新中找到一种方法式来更改它,现在您必须手工选择输出神经元的数量。
现在,我们调用完整的 MLP 函数,并查看输出,然后我会解释为了操作成为可能,已完成的工作。
LI 0 10:10:29.995 NNTestScript (#NQ100,H1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IF 0 10:10:29.995 NNTestScript (#NQ100,H1) biases EI 0 10:10:29.995 NNTestScript (#NQ100,H1) 0.6283 0.2029 0.1004 IQ 0 10:10:29.995 NNTestScript (#NQ100,H1) Hidden Layer 1 | Nodes 4 | Bias 0.6283 NS 0 10:10:29.995 NNTestScript (#NQ100,H1) Inputs 2 Weights 8 JD 0 10:10:29.995 NNTestScript (#NQ100,H1) 4.00000 6.00000 FL 0 10:10:29.995 NNTestScript (#NQ100,H1) 0.954 0.026 0.599 0.952 0.864 0.161 0.818 0.765 EJ 0 10:10:29.995 NNTestScript (#NQ100,H1) Arr size A 2 EM 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[0] = 3.81519 X A[0] = 4.000 B[0] = 0.954 NI 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[0] = 9.00110 X A[1] = 6.000 B[4] = 0.864 IE 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.10486 X A[0] = 4.000 B[1] = 0.026 DQ 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[1] = 1.06927 X A[1] = 6.000 B[5] = 0.161 MM 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[2] = 2.39417 X A[0] = 4.000 B[2] = 0.599 JI 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[2] = 7.29974 X A[1] = 6.000 B[6] = 0.818 GE 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[3] = 3.80725 X A[0] = 4.000 B[3] = 0.952 KQ 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[3] = 8.39569 X A[1] = 6.000 B[7] = 0.765 DL 0 10:10:29.995 NNTestScript (#NQ100,H1) before rows 1 cols 4 GI 0 10:10:29.995 NNTestScript (#NQ100,H1) IxWMatrix QM 0 10:10:29.995 NNTestScript (#NQ100,H1) Matrix CH 0 10:10:29.995 NNTestScript (#NQ100,H1) [ HK 0 10:10:29.995 NNTestScript (#NQ100,H1) 9.00110 1.06927 7.29974 8.39569 OO 0 10:10:29.995 NNTestScript (#NQ100,H1) ] CH 0 10:10:29.995 NNTestScript (#NQ100,H1) rows = 1 cols = 4 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< End of the first Hidden Layer >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> NS 0 10:10:29.995 NNTestScript (#NQ100,H1) Hidden Layer 2 | Nodes 6 | Bias 0.2029 HF 0 10:10:29.995 NNTestScript (#NQ100,H1) Inputs 4 Weights 24 LR 0 10:10:29.995 NNTestScript (#NQ100,H1) 0.99993 0.84522 0.99964 0.99988 EL 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.002 0.061 0.056 0.600 0.737 0.454 0.113 0.622 0.387 0.456 0.938 0.587 0.379 0.207 0.356 0.784 0.046 0.597 0.511 0.838 0.848 0.748 0.047 0.282 FF 0 10:10:29.996 NNTestScript (#NQ100,H1) Arr size A 4 EI 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.00168 X A[0] = 1.000 B[0] = 0.002 QE 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.09745 X A[1] = 0.845 B[6] = 0.113 MR 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.47622 X A[2] = 1.000 B[12] = 0.379 NN 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.98699 X A[3] = 1.000 B[18] = 0.511 MI 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.06109 X A[0] = 1.000 B[1] = 0.061 ME 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.58690 X A[1] = 0.845 B[7] = 0.622 PR 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.79347 X A[2] = 1.000 B[13] = 0.207 KN 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 1.63147 X A[3] = 1.000 B[19] = 0.838 GI 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 0.05603 X A[0] = 1.000 B[2] = 0.056 GE 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 0.38353 X A[1] = 0.845 B[8] = 0.387 GS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 0.73961 X A[2] = 1.000 B[14] = 0.356 CO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 1.58725 X A[3] = 1.000 B[20] = 0.848 KH 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 0.59988 X A[0] = 1.000 B[3] = 0.600 OD 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 0.98514 X A[1] = 0.845 B[9] = 0.456 LS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 1.76888 X A[2] = 1.000 B[15] = 0.784 KO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 2.51696 X A[3] = 1.000 B[21] = 0.748 PH 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 0.73713 X A[0] = 1.000 B[4] = 0.737 FG 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 1.53007 X A[1] = 0.845 B[10] = 0.938 RS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 1.57626 X A[2] = 1.000 B[16] = 0.046 OO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 1.62374 X A[3] = 1.000 B[22] = 0.047 EH 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 0.45380 X A[0] = 1.000 B[5] = 0.454 DG 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 0.95008 X A[1] = 0.845 B[11] = 0.587 PS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 1.54675 X A[2] = 1.000 B[17] = 0.597 EO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 1.82885 X A[3] = 1.000 B[23] = 0.282 KH 0 10:10:29.996 NNTestScript (#NQ100,H1) before rows 1 cols 6 RL 0 10:10:29.996 NNTestScript (#NQ100,H1) IxWMatrix HI 0 10:10:29.996 NNTestScript (#NQ100,H1) Matrix NS 0 10:10:29.996 NNTestScript (#NQ100,H1) [ ND 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.98699 1.63147 1.58725 2.51696 1.62374 1.82885 JM 0 10:10:29.996 NNTestScript (#NQ100,H1) ] LG 0 10:10:29.996 NNTestScript (#NQ100,H1) rows = 1 cols = 6 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< End of second Hidden Layer >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> ML 0 10:10:29.996 NNTestScript (#NQ100,H1) Hidden Layer 3 | Nodes 1 | Bias 0.1004 OG 0 10:10:29.996 NNTestScript (#NQ100,H1) Inputs 6 Weights 6 NQ 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.76671 0.86228 0.85694 0.93819 0.86135 0.88409 QM 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.278 0.401 0.574 0.301 0.256 0.870 RD 0 10:10:29.996 NNTestScript (#NQ100,H1) Arr size A 6 NO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.21285 X A[0] = 0.767 B[0] = 0.278 QK 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.55894 X A[1] = 0.862 B[1] = 0.401 CG 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 1.05080 X A[2] = 0.857 B[2] = 0.574 DS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 1.33314 X A[3] = 0.938 B[3] = 0.301 HO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 1.55394 X A[4] = 0.861 B[4] = 0.256 CJ 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 2.32266 X A[5] = 0.884 B[5] = 0.870 HF 0 10:10:29.996 NNTestScript (#NQ100,H1) before rows 1 cols 1 LR 0 10:10:29.996 NNTestScript (#NQ100,H1) IxWMatrix NS 0 10:10:29.996 NNTestScript (#NQ100,H1) Matrix DF 0 10:10:29.996 NNTestScript (#NQ100,H1) [ NN 0 10:10:29.996 NNTestScript (#NQ100,H1) 2.32266 DJ 0 10:10:29.996 NNTestScript (#NQ100,H1) ] GM 0 10:10:29.996 NNTestScript (#NQ100,H1) rows = 1 cols = 1
我来可视化网络,如此我们便可看到第一层上已完成的工作,其余的只是迭代完全相同的过程。
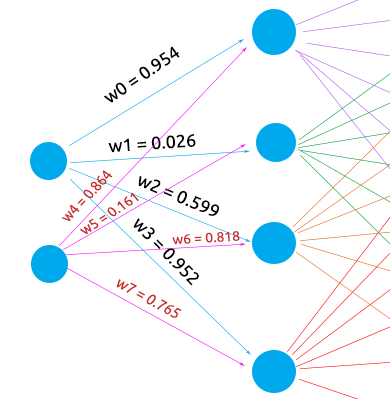
矩阵乘法已经能够精确地将第一层的权重乘以输入,如同它应该做的那样,但是,编码逻辑并不像听起来那么简单,事情可能会变得有点混乱,参阅下面的代码。 忽略其余代码,只需关注 MatrixMultiply 函数。
void CNeuralNets::FeedForwardMLP( double &MLPInputs[], double &MLPOutput[]) { //--- m_hiddenLayers = m_hiddenLayers+1; ArrayResize(m_hiddenLayerNodes,m_hiddenLayers); m_hiddenLayerNodes[m_hiddenLayers-1] = m_outputLayers; int HLnodes = ArraySize(MLPInputs); int weight_start = 0; double Weights[], bias[]; ArrayResize(bias,m_hiddenLayers); //--- int inputs=ArraySize(MLPInputs); int w_size = 0; //size of weights int cols = inputs, rows=1; double IxWMatrix[]; //dot product matrix //Generate random bias for(int i=0; i<m_hiddenLayers; i++) bias[i] = MathRandom(0,1); //generate weights int sum_weights=0, L_inputs=inputs; double L_weights[]; for (int i=0; i<m_hiddenLayers; i++) { sum_weights += L_inputs * m_hiddenLayerNodes[i]; ArrayResize(Weights,sum_weights); L_inputs = m_hiddenLayerNodes[i]; } for (int j=0; j<sum_weights; j++) Weights[j] = MathRandom(0,1); for (int i=0; i<m_hiddenLayers; i++) { w_size = (inputs*m_hiddenLayerNodes[i]); ArrayResize(L_weights,w_size); ArrayCopy(L_weights,Weights,0,0,w_size); ArrayRemove(Weights,0,w_size); MatrixMultiply(MLPInputs,L_weights,IxWMatrix,cols,cols,rows,cols); ArrayFree(MLPInputs); ArrayResize(MLPInputs,m_hiddenLayerNodes[i]); inputs = ArraySize(MLPInputs); for(int k=0; k<ArraySize(IxWMatrix); k++) MLPInputs[k] = ActivationFx(IxWMatrix[k]+bias[i]); } }
网络上输入层中的最先一个转化为一个 1xn 矩阵,意味着它是 1 行,但列数未知 (n)。 我们在这一行上的 “for” 循环之前,在外部初始化这个逻辑
int cols = inputs, rows=1;
为了获得完成乘法过程所需的总权重数,我们将输入层/上一层的数量乘以输出/下一层的数量,在这种情况下,我们在第一个隐藏层中有 2 个输入和 4 个节点,所以最后我们需要 2×4 = 8,八(8)个权重值。 更重要的技巧全可在这里找到:
MatrixMultiply(MLPInputs,L_weights,IxWMatrix,cols,cols,rows,cols);
为了很更好地理解这一点,我们看看矩阵乘法的作用:
void MatrixMultiply(double &A[],double &B[],double &AxBMatrix[], int colsA,int rowsB,int &new_rows,int &new_cols)
最后一个输入new_rows,new_cols 为新矩阵的行和列择选新的更新值,然后这些值在下一个矩阵里重用作行数和列数。 还记得,下一层的输入是上一层的输出吗?
这对于矩阵更为重要,因为
- 在第一层输入矩阵中是 1×2 权重矩阵 = 2×4 : 输出矩阵 = 1×4
- 在第二层输入矩阵 1×4 权重矩阵 = 4×6 : 输出矩阵 = 1×6
- 第三层输入 1×6 权重矩阵 6×1 输出矩阵 = 1×1
我们知道,矩阵相乘,第一个矩阵中的列数必须等于第二个矩阵中的行数。 结果矩阵的维度则是第一个矩阵的行数,和第二个矩阵的列数。
自上述操作
最先的第一个输入是具有已知维度的输入,但权重矩阵有 8 个元素,这些元素是通过将输入和隐藏层中的节点数相乘得来的,故此我们最终可以得出结论,它的行数等于前一层/输入中的列数,仅此而已。 将 new rows 和 new columns 的值修改为旧有数值的过程,会令此逻辑成为可能(内部矩阵相乘函数)
new_rows = rowsA; new_cols = colsB;
有关矩阵的更多信息,请尝试标准库里的矩阵部分,或您也许想尝试本文末尾链接的函数库中所用的其它不同之处。
现在我们拥有了一个灵活的架构,我们看看如何训练这个前馈 MLP 网络,以及训练和测试的可能样子。
涉及的过程
- 我们训练网络 x 个世代,来查找误差最小的模型。
- 我们把模型的参数存储在二进制文件中,这样我们就可在其它程序中读取该文件,例如在智能系统当中。
稍等一下,我刚才是说我们查找误差最少的模型吗?好吧,我们没有,这只是前馈。
MQL5.社区中的一些人更喜欢在输入上采用这些参数来优化 EA,这确实有效,但在其中,我们只生成一次权重和乖离,并在其余的世代中用到它们,就像我们在反向传播中所做的那样,但这里唯一的事情是,一旦设置了这些值,我们就不能更新它们, 它们不可更新 — 周期。
采用默认世代数,其设置为 1(一)。
void CNeuralNets::train_feedforwardMLP(double &XMatrix[],int epochs=1)
您可以找到一种方式来修改代码,并将权重置于脚本的输入上,您可以从那里将世代数设置为任何值,当然您也不必仅限于这种方式。 顺便说一下,这只是一个演示。
在从未见过的数据上测试或使用模型
为了能够使用训练过的模型,我们还需要能够与其它程序共享它的参数,这可以利用文件来实现,因为我们的模型参数是数组中的双精度值,故此二进制文件是我们需要的,我们从二进制文件里读取我们存储的权重和乖离,并将它们转存在各自的数组中备用。
好的,这里是负责训练神经网络的函数。
void CNeuralNets::train_feedforwardMLP(double &XMatrix[],int epochs=1) { double MLPInputs[]; ArrayResize(MLPInputs,m_inputs); double MLPOutputs[]; ArrayResize(MLPOutputs,m_outputLayers); double Weights[], bias[]; setmodelParams(Weights,bias); //Generating random weights and bias for (int i=0; i<epochs; i++) { int start = 0; int rows = ArraySize(XMatrix)/m_inputs; { if (m_debug) printf("<<<< %d >>>",j+1); ArrayCopy(MLPInputs,XMatrix,0,start,m_inputs); FeedForwardMLP(MLPInputs,MLPOutputs,Weights,bias); start+=m_inputs; } } WriteBin(Weights,bias); }
函数 setmodelParams() 是一个生成随机权重和乖离值的函数。 训练模型之后,我们得到权重和乖离值,然后将它们存储在二进制文件当中。
WriteBin(Weights,bias);
为了演示 MLP 中的一切都是如何操作的,我们将用此处找到的真实示例数据集。
参数 XMatrix[] 是我们训练模型时打算用到的所有输入值的矩阵,在这种情况下,我们需要将 CSV 文件导入矩阵。
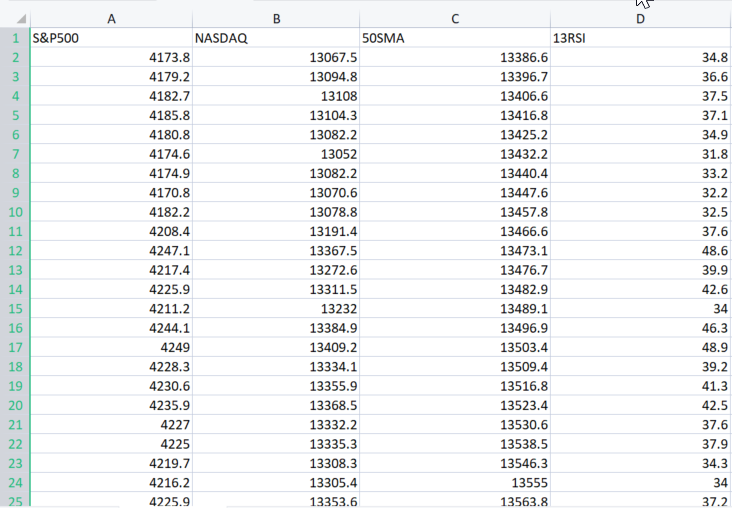
我们导入数据集
好吧,我帮您做到了。
double XMatrix[]; int rows,cols; CSVToMatrix(XMatrix,rows,cols,"NASDAQ_DATA.csv"); MatrixPrint(XMatrix,cols,3);
上述代码片段的输出:
MN 0 12:02:13.339 NNTestScript (#NQ100,H1) Matrix MI 0 12:02:13.340 NNTestScript (#NQ100,H1) [ MJ 0 12:02:13.340 NNTestScript (#NQ100,H1) 4173.800 13067.500 13386.600 34.800 RD 0 12:02:13.340 NNTestScript (#NQ100,H1) 4179.200 13094.800 13396.700 36.600 JQ 0 12:02:13.340 NNTestScript (#NQ100,H1) 4182.700 13108.000 13406.600 37.500 FK 0 12:02:13.340 NNTestScript (#NQ100,H1) 4185.800 13104.300 13416.800 37.100 ..... ..... ..... DK 0 12:02:13.353 NNTestScript (#NQ100,H1) 4332.700 14090.200 14224.600 43.700 GD 0 12:02:13.353 NNTestScript (#NQ100,H1) 4352.500 14162.000 14225.000 47.300 IN 0 12:02:13.353 NNTestScript (#NQ100,H1) 4401.900 14310.300 14226.200 56.100 DK 0 12:02:13.353 NNTestScript (#NQ100,H1) 4405.200 14312.700 14224.500 56.200 EE 0 12:02:13.353 NNTestScript (#NQ100,H1) 4415.800 14370.400 14223.200 60.000 OS 0 12:02:13.353 NNTestScript (#NQ100,H1) ] IE 0 12:02:13.353 NNTestScript (#NQ100,H1) rows = 744 cols = 4
现在整个 CSV 文件都被转存到 XMatrix[] 中。 干杯!
这个结果矩阵的好处在于您不必再担心神经网络的输入,因为变量 cols 从 Csv 文件中获取列数。 这些将成为神经网络的输入。 那么最后,这是整个脚本的样子:
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ #include "NeuralNets.mqh"; CNeuralNets *neuralnet; //+------------------------------------------------------------------+ void OnStart() { int hlnodes[3] = {4,6,1}; int outputs = 1; int inputs_=2; double XMatrix[]; int rows,cols; CSVToMatrix(XMatrix,rows,cols,"NASDAQ_DATA.csv"); MatrixPrint(XMatrix,cols,3); neuralnet = new CNeuralNets(SIGMOID,RELU,cols,hlnodes,outputs); neuralnet.train_feedforwardMLP(XMatrix); delete(neuralnet); }
简单吧? 但我们仍然需要修复几行代码,在 train_feedforwardMLP 内部,我们在单次世代迭代中添加整个数据集的迭代,这是为了完整地表示一个世代的含义。
for (int i=0; i<epochs; i++) { int start = 0; int rows = ArraySize(XMatrix)/m_inputs; for (int j=0; j<rows; j++) //iterate the entire dataset in a single epoch { if (m_debug) printf("<<<< %d >>>",j+1); ArrayCopy(MLPInputs,XMatrix,0,start,m_inputs); FeedForwardMLP(MLPInputs,MLPOutputs,Weights,bias); start+=m_inputs; } }
现在我们看看在调试模式下运行此程序时的日志。
bool m_debug = true;
调试模式也许会塞满您的硬盘空间,除非您正在调试神经网络,最好将其设置为 false;我运行过一次程序,我的日志占用了多达 21Mb 的空间。
两次迭代的简要概览:
MR 0 12:23:16.485 NNTestScript (#NQ100,H1) <<<< 1 >>> DE 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden layer nodes plus the output FS 0 12:23:16.485 NNTestScript (#NQ100,H1) 4 6 1 1 KK 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden Layer 1 | Nodes 4 | Bias 0.3903 IN 0 12:23:16.485 NNTestScript (#NQ100,H1) Inputs 4 Weights 16 MJ 0 12:23:16.485 NNTestScript (#NQ100,H1) 4173.80000 13067.50000 13386.60000 34.80000 DF 0 12:23:16.485 NNTestScript (#NQ100,H1) 0.060 0.549 0.797 0.670 0.420 0.914 0.146 0.968 0.464 0.031 0.855 0.240 0.717 0.288 0.372 0.805 .... PD 0 12:23:16.485 NNTestScript (#NQ100,H1) MLP Final Output LM 0 12:23:16.485 NNTestScript (#NQ100,H1) 1.333 HP 0 12:23:16.485 NNTestScript (#NQ100,H1) <<<< 2 >>> PG 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden layer nodes plus the output JR 0 12:23:16.485 NNTestScript (#NQ100,H1) 4 6 1 1 OH 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden Layer 1 | Nodes 4 | Bias 0.3903 EI 0 12:23:16.485 NNTestScript (#NQ100,H1) Inputs 4 Weights 16 FM 0 12:23:16.485 NNTestScript (#NQ100,H1) 4179.20000 13094.80000 13396.70000 36.60000 II 0 12:23:16.486 NNTestScript (#NQ100,H1) 0.060 0.549 0.797 0.670 0.420 0.914 0.146 0.968 0.464 0.031 0.855 0.240 0.717 0.288 0.372 0.805 GJ 0 12:23:16.486 NNTestScript (#NQ100,H1)
一切都已设置完毕,并按预期运行良好。 现在,我们将模型参数存储在二进制文件之中。
模型参数存储在二进制文件之中
bool CNeuralNets::WriteBin(double &w[], double &b[]) { string file_name_w = NULL, file_name_b= NULL; int handle_w, handle_b; file_name_w = MQLInfoString(MQL_PROGRAM_NAME)+"\"+"model_w.bin"; file_name_b = MQLInfoString(MQL_PROGRAM_NAME)+"\"+"model_b.bin"; FileDelete(file_name_w); FileDelete(file_name_b); handle_w = FileOpen(file_name_w,FILE_WRITE|FILE_BIN); if (handle_w == INVALID_HANDLE) { printf("Invalid %s Handle err %d",file_name_w,GetLastError()); } else FileWriteArray(handle_w,w); FileClose(handle_w); handle_b = FileOpen(file_name_b,FILE_WRITE|FILE_BIN); if (handle_b == INVALID_HANDLE) { printf("Invalid %s Handle err %d",file_name_b,GetLastError()); } else FileWriteArray(handle_b,b); FileClose(handle_b); return(true); }
这一步超级重要。 如前所述,它有助于与其它采用同一函数库的程序共享模型参数。 二进制文件将保存在以您的脚本文件名命名的子目录当中:
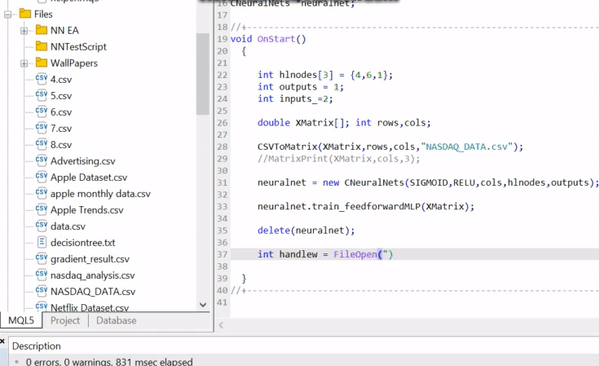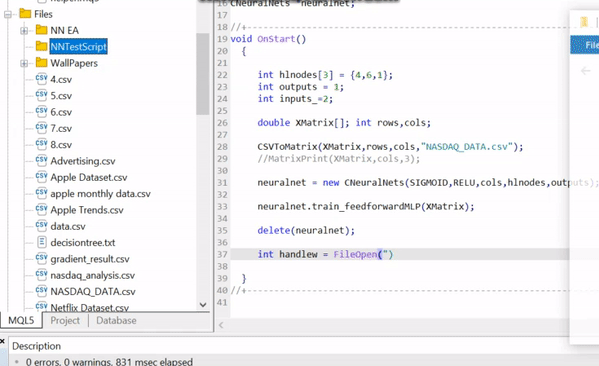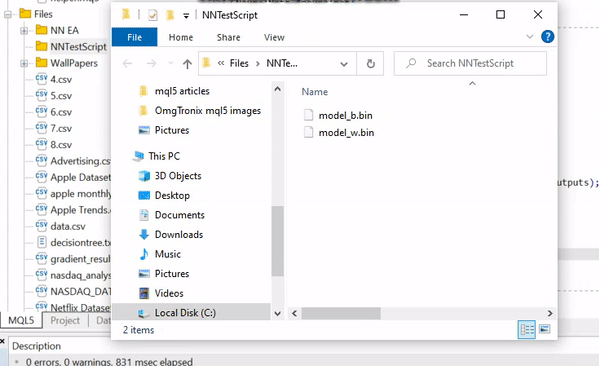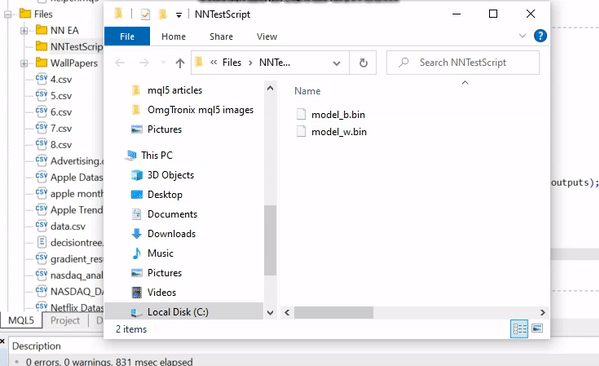
有关如何在其它程序中访问模型参数的示例:
double weights[], bias[]; int handlew = FileOpen("NNTestScript\model_w.bin",FILE_READ|FILE_BIN); FileReadArray(handlew,weights); FileClose(handlew); int handleb = FileOpen("NNTestScript\model_b.bin",FILE_READ|FILE_BIN); FileReadArray(handleb,bias); FileClose(handleb); Print("bias"); ArrayPrint(bias,4); Print("Weights"); ArrayPrint(weights,4);
输出:
HR 0 14:14:02.380 NNTestScript (#NQ100,H1) bias DG 0 14:14:02.385 NNTestScript (#NQ100,H1) 0.0063 0.2737 0.9216 0.4435 OQ 0 14:14:02.385 NNTestScript (#NQ100,H1) Weights GG 0 14:14:02.385 NNTestScript (#NQ100,H1) [ 0] 0.5338 0.6378 0.6710 0.6256 0.8313 0.8093 0.1779 0.4027 0.5229 0.9181 0.5449 0.4888 0.9003 0.2870 0.7107 0.8477 NJ 0 14:14:02.385 NNTestScript (#NQ100,H1) [16] 0.2328 0.1257 0.4917 0.1930 0.3924 0.2824 0.4536 0.9975 0.9484 0.5822 0.0198 0.7951 0.3904 0.7858 0.7213 0.0529 EN 0 14:14:02.385 NNTestScript (#NQ100,H1) [32] 0.6332 0.6975 0.9969 0.3987 0.4623 0.4558 0.4474 0.4821 0.0742 0.5364 0.9512 0.2517 0.3690 0.4989 0.5482
太棒了,您现在可以从任何地方访问该文件,只要您知道名称,以及在哪里可以找到它们。
使用模型
这是最容易的部分。 前馈 MLP 函数已修改,添加了新的权重和乖离输入,这将有助于运行模型,从而获取最近的价格数据,或其它什么东西。
void CNeuralNets::FeedForwardMLP(double &MLPInputs[],double &MLPOutput[],double &Weights[], double &bias[])
有关如何提取权重和乖离,并实时使用模型的完整代码。 首先我们读取参数,然后插入输入值,而非输入矩阵,因为这次我们用经过训练的模型来预测输入值的结果。 MLPOutput[] 为您提供输出数组:
double weights[], bias[]; int handlew = FileOpen("NNTestScript\model_w.bin",FILE_READ|FILE_BIN); FileReadArray(handlew,weights); FileClose(handlew); int handleb = FileOpen("NNTestScript\model_b.bin",FILE_READ|FILE_BIN); FileReadArray(handleb,bias); FileClose(handleb); double Inputs[]; ArrayCopy(Inputs,XMatrix,0,0,cols); //copy the four first columns from this matrix double Output[]; neuralnet = new CNeuralNets(SIGMOID,RELU,cols,hlnodes,outputs); neuralnet.FeedForwardMLP(Inputs,Output,weights,bias); Print("Outputs"); ArrayPrint(Output); delete(neuralnet);
理应工作正常。
现在,您可以随意探索各种架构,并探索不同的选项,看看什么最适合您。
前馈神经网络是第一个,也是最简单的人工神经网络类型。 在这个网络中,信息只在一个方向上移动 — 向前移动 — 从输入节点,经过隐藏节点(如果有的话),到输出节点。 网络中没有循环或回路
我们刚刚编写的这个模型是一个基本的模型,除非优化(我 100% 确定),否则不一定能为您提供期望的结果,希望您能发挥创造力,并从中有所作为。
最终思考
理解每种机器学习技术的理论,以及紧闭门户之后的所有内容非常重要,因为我们在 MQL5 中没有数据科学软件包,好在至少我们有 python 框架,但有时我们可能需要在 MetaTrader 中工作,如果没有对这些事情背后的理论有扎实的理解,一个人会很难理清事情,并难以充分利用机器学习,随着我们深入了解理论的重要性,我们在系列文章前面讨论的内容被证明非常重要。
此致敬礼。
GitHub 存储库: https://github.com/MegaJoctan/NeuralNetworks-MQL5
参阅更多关于我的矩阵和向量函数库的信息
延伸阅读 | 书籍 | 参考
- 用于模式识别的神经网络(计量经济学中的高级文本)
- 神经网络:交易的技巧(计算机科学讲义,7700)
- 深度学习(自适应计算和机器学习系列)
文章参考资料:
- 数据科学和机器学习(第 01 部分):线性回归
- 数据科学和机器学习(第 02 部分):逻辑回归
- 数据科学和机器学习(第 03 部分):矩阵回归
- 数据科学和机器学习(第 06 部分):梯度下降
- 数据科学与机器学习 — 神经网络(第 01 部分):前馈神经网络解密
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/11334
MyFxtops迈投(www.myfxtops.com)-靠谱的外汇跟单社区,免费跟随高手做交易!
免责声明:本文系转载自网络,如有侵犯,请联系我们立即删除,另:本文仅代表作者个人观点,与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。

 MyFxTops邁投財經
MyFxTops邁投財經
