简介

本文重点介绍机器学习模型中输入变量（预测因子）的选择，预处理以及评估的相关细节。多种规范化的方法以及它们的特点都将在此被讨论。在处理过程中将极大影响模型训练最终结果的环节也将在此探讨。我们将仔细看看，并评估新的及鲜为人知的用于确定输入数据信息量和可视化的方法。

我们将使用“RandomUniformForests”包，计算并分析变量不同值和各种组合的重要概念，预测因子和目标的对应关系，预测因子之间的相互作用，以及将所有重要的方面都考虑在内后预测因子集的最优选取。

我们将使用“RoughSets”包，换一个角度和基于其他概念来探讨预测因子的选择问题。我们将揭示不仅是预测因子集可以被优化，用于训练的样本集也可以被优化。

所有的计算和实验将用R语言来实现，准确的说是用 — Revolution R Open 3.2.1。

1. 输入变量（符号，预测因子）

所有的变量，输入（独立的，预测因子）和输出（目标）可以是下面的类型：

• 二元值 — 有两个值的： {0,1}, {-1,1}, {“yes”, “no”}, {“male”, “female”}。

• 有限数量种类的要素（因子）。例如，因子“星期几”有七个类别，诶一种都可以被命名（星期一、星期二等等）。因子可以是有序的或者是无序的。例如，因子“一天中的小时”有24个类别并且是有序的。因子“一个城市的区”有32个但是无序的，因为每一个类别都是同等重要的。当生命一个有序因子是需要清晰的指出。

• 量化（数字化的）连续值。连续变量的范围从负Inf（无穷）到+Inf。

“原始”报价数据（OHLC）不作为数值输入变量。应用差异对数或者报价比对数。然而，各种指标组合作为输入变量集是最常用的方式。通常，将输入数据集作为矩阵形式组织，如果所有变量都是规整的，或者更一般的，作为一个数据帧，每一列是一个变量，每一行是变量在某一特定时刻的状态。目标变量放在最后（或最先）的列上。

1.1. 清理

清理意味着：

a) 移除或者转换丢失（不确定的）的数据 “NA”。

许多模型不允许输入数据出现缺失。因此，我们或者删除丢失的数据行或者用插值数据将缺口填充。实现这类目标的函数在很多包中都有提供。移除不确定的数据NA的操作通常是默认，但最好还是在开始训练前由你亲自通过na.omit(dt) 来实现。

b) 移除异常值（数值的或者字符的）。

在某些情况下（尤其是在变量的转换或者变换过程中）预测因子可能以单一异常值或者几个这类值的形式非常低频率的出现。对于很多模型，这种情况会使得操作不稳定甚至崩溃。这些接近零方差的预测因子必须在仿真前被确定及去除。为了确定和去除这类预测因子，可以使用 “caret” 包中的一个特殊的函数：caret::nearZeroVar()。这一点是否有必要可以再探讨。

c) 确定并移除相关因子（数值的）。

某些模型在处理相关预测因子时尤为出色（例如PLS、LARS和使用规范化L1的类似模型），而其他模型能够从减少因子之间的相关性水平上获益。要识别和移除强相关预测因子（设置相关系数阈值，例如 > 0.9）， 我们使用”caret”包中的caret::findCorrelation() 函数。这个包功能非常强大，我强烈建议对其进行分析。

d) 识别并去除线性相关性（要素）。

caret::findLinearCombos() 函数使用矩阵转换的QR-扩展来罗列它们的线性组合（如果存在）。例如，让我们分析下面的矩阵：

ltfrDesign <- matrix(0, nrow = 6, ncol = 6)
ltfrDesign[, 1] <- c(1, 1, 1, 1, 1, 1)
ltfrDesign[, 2] <- c(1, 1, 1, 0, 0, 0)
ltfrDesign[, 3] <- c(0, 0, 0, 1, 1, 1)
ltfrDesign[, 4] <- c(1, 0, 0, 1, 0, 0)
ltfrDesign[, 5] <- c(0, 1, 0, 0, 1, 0)
ltfrDesign[, 6] <- c(0, 0, 1, 0, 0, 1)

请注意第2、3列加起来就是第1列。类似的，第4、5、6列加起来就是第1列。caret::findLinearCombos() 函数将返回将沿着列向量的位置枚举的相关性列表，它们可以被删除以去除线性相关性。

comboInfo <- findLinearCombos(ltfrDesign)
comboInfo
$linearCombos
$linearCombos[[1]]
[1] 3 1 2
$linearCombos[[2]]
[1] 6 1 4 5
$remove
[1] 3 6
ltfrDesign[, -comboInfo$remove]
     [,1] [,2] [,3] [,4]
[1,]    1    1    1    0
[2,]    1    1    0    1
[3,]    1    1    0    0
[4,]    1    0    1    0
[5,]    1    0    0    1
[6,]    1    0    0    0

这种相关性可能发生在当使用大量二元预测因子或者当预测因子被转换成 “虚拟变量”时。

1.2. 转换，数据预处理

许多模型需要在某一特定该范围内（规范化、标准化）的数值型输入数据，或者以某种方式（要素）进行转换。例如，神经网络和支持向量机（SVM）接受的输入数据范围在[-1, 1] 或 [0, 1]。R语言中的许多包为这种转换提供特定的功能或者本身就能执行这类变换。请记住预处理参数的定义仅仅在输入数据的训练集上进行。测试和效验集，新数据，产生的预测模型使用训练集上获得的参数来进行转换。

标准化（缩放）

将一个变量准换到{+ h, -l}范围内的一般公式。取决于目标范围 h = +1; l = (-1 或 0)。有些人建议将目标范围收缩到{-0.9; 0.9}或{0.1; 0.9}，以避免使用激活函数(tanh/sig)的逼近极值部分。这同神经网络，SVM和其他使用此类激活函数的模型有关。

逆变换（反规范化）的公式如下：

标准化

已知变量的分布接近均匀分布，则可以使用下面的公式来标准化：

某些包中有特定的函数用于预处理。因此，“caret”包中的preProcess()函数提供如下预处理方法：”BoxCox”, “YeoJohnson”, “expoTrans”, “center”, “scale”, “range”, “knnImpute”, “bagImpute”, “medianImpute”, “pca”, “ica” 和 “spatialSign”。

“BoxCox”, “YeoJohnson”, “expoTrans”

Yeо-Johnson变换和Box-Cox模型有些类似，但是它可以接受为零或负值的预测因子（而Box-Cox变换的预测因子必须严格为正）。Manly(1976)指数变换也可以被用于正数或负数的变换。

“range” 数据转换范围在[0, 1]内。这非常重要！如果新的样本中有大于或者小于训练集中的数据，那么它们转换后可能落在此范围外，预测结果就可能失真。

“center” — 减去平均值，“scale” 除以标准差（尺度）。通常它们一起使用，称为：“标准化”。

“knnImpute”, “bagImpute”, “medianImpute” — 使用不同的算法计算缺失或者未定义数据。

“spatialSign” — 变换，将预测因子数据映射到р维单位圆上，其中р是预测因子的数量。本质上是矢量数据除以它的模。在转换前数据必须先中心化和尺度化。

“pca” — 在某些情况下，必须用主成分分析将数据变换到一个较小的子空间中，在这个空间内新的变量彼此不相关。使用这个而方法，中心化和尺度化自动被执行，列的名称改为PC1，PC2，等。

“isa” — 类似的，独立分量分析可用于发现是原始集合线性组合的新变量，其中分量是独立的（和PCA中的非相关性不同）。新的变量将被标识为 IC1，IC2，等。

“clusterSim”是一个优秀的用于寻找最佳数据聚类过程的包，其中dataNormalization() 函数能以18种方式按行和列规范化数据。我将它们简单罗列在此：

• n1 — 标准化 ((x – mean) / sd)；

• n2 — 位置标准化 ((x – median) / mad)；

• n3 — 归一化 ((x – mean) / range)；

• n3а — 位置归一化 ((x – median) / range)；

• n4 — 用最小值归一化 ((x – min) / range)；

• n5 — 在<-1, 1>范围内标准化 ((x – mean) / max(abs(x – mean)))；

• n5a — 在<-1,1>范围内位置标准化 ((x – median) / max(abs(x-median)))；

• n6 — 商变换 (x/sd)；

• n6a — 位置商变换 (x/mad)；

• n7 — 商变换 (x/range)；

• n8 — 商变换 (x/max)；

• n9 — 商变换 (x/mean)；

• n9a — 位置商变换 (x/median)；

• n10 — 商变换 (x/sum)；

• n11 — 商变换 (x/sqrt(SSQ))；

• n12 — 标准化 ((x-mean)/sqrt(sum((x-mean)^2)))；

• n12a — 位置标准化 ((x-median)/sqrt(sum((x-median)^2)))；

• n13 — 零位于中心点的标准化 ((x-midrange)/(range/2))。

“Dummy Variables” – 许多模型需要转换预测因子为“虚拟”变量。“caret” 包中的函数dummyVar() 可用于实现此目标。该函数使用公式和数据集，并显示可用于创建虚拟变量的对象。

2. 输出变量（目标变量）

因为我们要解决分类问题，目标变量是一个具有多种级别（种类）的因子。当训练有两个类别的目标时，大多数模型的结果还不错。通过附加的手段，采用许多特殊的类来解决这类问题。目标变量在训练数据准备阶段被编码，并在预测后被解码。

分类有多种编码方式。“Stuttgart大学的神经网络仿真”RSNNS包中提供了两个函数 — decodeClassLabels() ，对包含对应类别的矩阵中的列向量进行编码，以及 encodeClassLabels()函数，它用于在模型预测之后进行逆变换。例如：

> data(iris)
> labels <- decodeClassLabels(iris[,5])
> class <- encodeClassLabels(labels)
> head(labels)
     setosa versicolor virginica
[1,]      1          0         0
[2,]      1          0         0
[3,]      1          0         0
[4,]      1          0         0
[5,]      1          0         0
[6,]      1          0         0
> head(class)
[1] 1 1 1 1 1 1

因此，模型的输出数量等于目标分类的数量。这并不是目标变量唯一的编码方式。如果目标有两个类别，你可以用一个输出值来处理。在矩阵中对目标变量进行编码有许多好处。

3. 预测因子的评估和选择

实验证明增加输入数据（预测因子）并不能总是提升模型的质量，相反可能会使模型变坏。模型的结果实际上受3-5种预测因子的影响。在许多聚合包中，如”rminer”，”caret”，”SuperLearner” 和 “mlr” ，有内置的用于计算变量重要性和变量选择的函数。大部分缩减预测因子的方法都可以被分为两类（根据 John, Kohavi and Pfleger, 1994 的提法）：

• 过滤。过滤方法评估预测模型外的预测因子相关性，并且，最终模型仅仅使用满足特定条件的预测因子。例如，对于分类任务而言每个预测因子都能被独立评估，检查其同观测分类之间的模糊关系。只有那些有明显相关性的预测因子才会被包含到分类模型中。

• 封装。用封装方法评估不同的模型，使用程序添加或删除预测因子来找到最佳组合以优化模型效率。实际上，封装方法是搜索算法，它将预测因子作为输入并使用要优化的模型的效率作为输出。有许多迭代预测因子的方法（递归移除/添加，遗传算法，模拟退火等等）。

这些方法都有各自的优点和缺点。一般来说，过滤法比封装法更加有效，但是选择标准不直接涉及该模型的效率。封装法的缺点是评估多模型（可能需要调整模型参数）会导致计算时间和模型重训练次数大大增加。

在本文中我们不考虑封装法，反之我们将分析过滤模型的新方法，在我看来能够去除所有上面提到的缺点。

3.1. 过滤

在使用了各种外部方法和标准后，预测因子的重要性（信息容量）被建立起来。在改进预测模型质量中每个变量的贡献度在此以重要度来表征。

这之后，一般来说有三种选择：

1. 选择重要度最高的特定数量的预测因子。

2. 从所有预测因子中选择一定个百分比的重要度最高的因子。

3. 选择重要度超过阈值的预测因子。

所有情况下，都可以对其中的数量，百分比和阈值进行优化。

让我们准备输入和输出数据集用于评估特定的方法以及进行试验。

输入数据

我们将采用11个指标（振荡器），在输入设置中不设优先级。我们将从某些指标中抽取多个变量。然后我们将写一个函数形成17个变量的输入集。

最近4000个 TF = M30 / EURUSD 柱形的报价将被采用。

In <- function(p = 16){
  require(TTR)
  require(dplyr)
  require(magrittr)
  adx <- ADX(price, n = p) %>% as.data.frame %>% 
          mutate(.,oscDX = DIp -DIn) %>% 
          transmute(.,DX, ADX, oscDX) %>% as.matrix()
  ar <- aroon(price[ ,c('High', 'Low')], n = p)%>% 
          extract(,3)
  atr <- ATR(price, n = p, maType = "EMA") %>%
          extract(,1:2)
  cci <- CCI(price[ ,2:4], n = p)
  chv <- chaikinVolatility(price[ ,2:4], n = p)
  cmo <- CMO(price[ ,'Med'], n = p)
  macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% 
          as.data.frame() %>% 
          mutate(., vsig = signal %>% 
          diff %>% c(NA,.) %>% multiply_by(10)) %>% 
          transmute(., sign = signal, vsig) %>% 
          as.matrix()
  rsi <- RSI(price[ ,'Med'], n = p)
  stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA")%>%
      as.data.frame() %>% mutate(., oscK = fastK - fastD)%>%
      transmute(.,slowD, oscK)%>% as.matrix()
  smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9)
  vol <- volatility(price[ ,1:4], n = p, calc = "yang.zhang", N = 144)
  In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, vol)
  return(In)
}

这些指标是非常知名且被广泛使用的，因此我们不在此赘述指标本身。我将基于MACD指标样例简单介绍“magrittr”包中的”pipe”(%>%) 计算方法。步骤如下：

1. 计算返回两个变量(macd, signal)的指标。

2. 获得的矩阵被转换为数据帧。

3. 一个新的变量vsig被添加到数据帧中（按顺序）：

   1. 采用signal 变量；
   2. 计算第一个差值；
   3. NA向量被添加到开始处，因为当计算第一个差值时此向量比初始值少一个单位；
   4. 乘以10。

4. 只有我们需要的变量（列）vsig, signal被从数据帧中选出来。

5. 数据帧转换为矩阵。

在不需要中间结果的情况下，此算法非常便捷。另外，公式易于读懂和理解。

我们将获取输入数据的矩阵并观察其中的内容。

x <- In(p = 16)
> summary(x)
       DX                ADX             oscDX        
 Min.   : 0.02685   Min.   : 5.291   Min.   :-93.889  
 1st Qu.: 8.11788   1st Qu.:14.268   1st Qu.: -9.486  
 Median :16.63550   Median :18.586   Median :  5.889  
 Mean   :20.70162   Mean   :20.716   Mean   :  4.227  
 3rd Qu.:29.90428   3rd Qu.:24.885   3rd Qu.: 19.693  
 Max.   :79.80812   Max.   :59.488   Max.   : 64.764  
 NA's   :16         NA's   :31       NA's   :16       
       ar                  tr                 atr          
 Min.   :-100.0000   Min.   :0.0000000   Min.   :0.000224  
 1st Qu.: -50.0000   1st Qu.:0.0002500   1st Qu.:0.000553  
 Median :  -6.2500   Median :0.0005600   Median :0.000724  
 Mean   :  -0.8064   Mean   :0.0008031   Mean   :0.000800  
 3rd Qu.:  50.0000   3rd Qu.:0.0010400   3rd Qu.:0.000970  
 Max.   : 100.0000   Max.   :0.0150300   Max.   :0.003104  
 NA's   :16          NA's   :1           NA's   :16        
      cci                chv                cmo          
 Min.   :-515.375   Min.   :-0.67428   Min.   :-88.5697  
 1st Qu.: -84.417   1st Qu.:-0.33704   1st Qu.:-29.9447  
 Median :  -5.674   Median : 0.03057   Median : -2.4055  
 Mean   :  -1.831   Mean   : 0.11572   Mean   : -0.6737  
 3rd Qu.:  83.517   3rd Qu.: 0.44393   3rd Qu.: 28.0323  
 Max.   : 387.814   Max.   : 3.25326   Max.   : 94.0649  
 NA's   :15         NA's   :31         NA's   :16        
      sign               vsig               rsi       
 Min.   :-0.38844   Min.   :-0.43815   Min.   :12.59  
 1st Qu.:-0.07124   1st Qu.:-0.05054   1st Qu.:39.89  
 Median :-0.00770   Median : 0.00009   Median :49.40  
 Mean   :-0.00383   Mean   :-0.00013   Mean   :49.56  
 3rd Qu.: 0.05075   3rd Qu.: 0.05203   3rd Qu.:58.87  
 Max.   : 0.38630   Max.   : 0.34871   Max.   :89.42  
 NA's   :33         NA's   :34         NA's   :16     
     slowD             oscK                SMI         
 Min.   :0.0499   Min.   :-0.415723   Min.   :-74.122  
 1st Qu.:0.2523   1st Qu.:-0.043000   1st Qu.:-33.002  
 Median :0.4720   Median : 0.000294   Median : -5.238  
 Mean   :0.4859   Mean   :-0.000017   Mean   : -4.089  
 3rd Qu.:0.7124   3rd Qu.: 0.045448   3rd Qu.: 22.156  
 Max.   :0.9448   Max.   : 0.448486   Max.   : 75.079  
 NA's   :19       NA's   :17          NA's   :25       
     signal             vol          
 Min.   :-71.539   Min.   :0.003516  
 1st Qu.:-31.749   1st Qu.:0.008204  
 Median : -5.319   Median :0.011274  
 Mean   : -4.071   Mean   :0.012337  
 3rd Qu.: 19.128   3rd Qu.:0.015312  
 Max.   : 71.695   Max.   :0.048948  
 NA's   :33        NA's   :16    

输出数据（目标）

作为目标变量，我们将使用ZigZag信号。下面就是计算zigzag和其信号的公式：

ZZ <- function(pr = price, ch = ch , mode="m") {
  require(TTR)
  if(ch > 1) ch <- ch/(10 ^ (Dig - 1))
  if(mode == "m"){pr <- pr[ ,'Med']}
  if(mode == "hl") {pr <- pr[ ,c("High", "Low")]}
  if(mode == "cl") {pr <- pr[ ,c("Close")]}
  zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T)
  n <- 1:length(zz)
  for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1]}
  dz <- zz %>% diff %>% c(0,.)
  sig <- sign(dz)
  return(cbind(zz, sig))
}

函数参数：

• pr = price — OHLCMed 报价的矩阵；
• ch — zigzag折线的最小长度，以点数计(4 signs)；
• mode — 应用的价格（m — 均价，hl — 最高最低价，cl — 收盘价）。默认使用均价。

函数返回有两个变量的矩阵 — zigzag和基于zigzag折线角度获得的信号，在[-1; 1]范围内。

我们用不同的leg长度计算两个ZZ信号：

out1 <- ZZ(ch = 25)
out2 <- ZZ(ch = 50)

图中它们看上去像这样：

> matplot(tail(cbind(out1[ ,1], out2[ ,1]), 500), t="l")

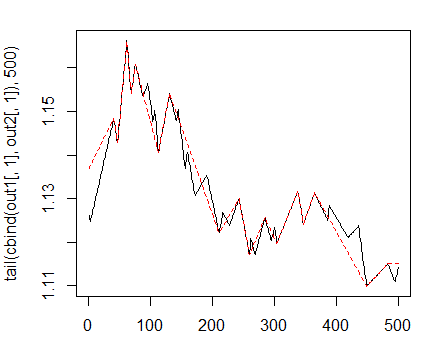
图 1. 折线最小长度 25/75 p 的Zigzags

接下来我们将使用第一个ZZ并采用更短的leg。我们打算将输入和目标变量组合到一般数据帧中，移除condition = “0”的未定义数据并且从目标变量中移除“0”类型。

> data <- cbind(as.data.frame(x) , Class = factor(out1[ ,2])) %>% 
+               na.omit
> data <- data[data$Class != 0, ]
> data$Class <- rminer::delevels(data$Class, c("0", "1"), "1")

查看目标的类型分布：

> table(data$Class)

  -1    1 
1980 1985 

从中可见，分类数量很均衡。既然我们已经准备好了输入和输出数据集，我们就能开始评估预测因子的重要性了。

首先我们检查输入数据的相关性：

> descCor <- cor(data[ ,-ncol(data)])
> summary(descCor[upper.tri(descCor)])
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
-0.20170  0.03803  0.26310  0.31750  0.57240  0.95730 

那两个输入变量的相关性超过了90%？

> highCor <- caret::findCorrelation(descCor, cutoff = .90)
> highCor
[1] 12 15

答案是 — rsi 和 SMI。我们将这连个排除后形成一个而数据集并观察剩余因子的相关性。

> data.f <- data[ ,-highCor]
> descCor <- cor(data.f[ ,-ncol(data.f)])
> summary(descCor[upper.tri(descCor)])
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
-0.20170  0.03219  0.21610  0.27060  0.47820  0.89880 

要评估变量的重要度(VI) 我们将使用一个新的包 “Random Uniform Forests”，其中含有大量的用于深度分析和可视化重要度的工具。作为此包开发者的目的之一，确定变量重要度的主要目标是找到它们何种，何时，何处以及如何影响我们待解决的问题。

这个包中提供了许多变量重要度评估的方法。在进行深入评估前我们先来了解一下它们。

全局变量重要度 将能减少预测误差的变量设置为最高等级，但它无法告诉我们此重要变量对结果的影响。

例如，我们希望知道哪个变量对独立分类影响更大，或者说变量之间的相互影响是什么。

变量的重要性通过所有的单元和树进行检测，所有变量都要有一个值，分割点是随机的。因此，每个变量都有相同的被选中的机会，要被认为是重要的变量，只有当它能最大程度的降低每个节点的误差。

局部变量 重要度

定义：如果对于同样的观测值和所有的树，它是在节点中出现频率最高的，那么我们认为此预测因子是一阶本地重要的。

局部 重要度

定义：如果对于同样的观测值、分类并在所有顺序中它是节点中出现频率最高的，那么我们认为此因子是局部重要的。

相互影响

我们想要知道预测因子是如何影响待解决问题的。例如，某些因子对目标的影响很低，但是可能会对更多相关变量产生很大影响，或者一个变量可能对其他变量有很大的影响。让我们定义下什么叫做互相影响。

定义：如果对于相同的观测值以及所有树，在终端节点上两者分别有一阶和二阶的最高出现频率，那么我们称预测因子有相互影响。

部分依赖

这些就是在已知所有其它变量值的情况下，确定一个（或一组）变量是如何对结果值产生影响的工具。为了更为明确，部分依赖是指基于响应值的变量能产生最大影响的区域。部分依赖的概念源于Friedman (2002)，他在梯度推进机(GBM)中使用，然而在Random Uniform Forests中的实现方式有所不同。

根据Random Uniform Forests包，我们可以根据下述方式确定变量的重要度： Importance = contribution + interaction，其中contribution 是变量对于预测误差的影响力（针对整体的影响），interaction 是对于其他变量的影响。

让我们继续进行实验

我们将按2：3的比例，把数据集data.f[]分成训练集和测试集，并且将数据规范化到-1：1范围内同时进行模型测试。我们使用rminer::holdout() 函数进行数据分组，将数据集一分为二。使用caret::preProcess() 函数和method = c(“spatialSign”)做数据规范化。当进行模型训练时，使用”doParallel”包将在可用的处理器内核间自动采用并行计算模式。你可以使用threads” 选项来指定要用于计算的特定内核数量”。

> idx <- rminer::holdout(y = data.f$Class)
> prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)],
+             method = c("spatialSign"))
> x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
> x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
> y.train <- data.f[idx$tr, ncol(data.f)]
> y.test <- data.f[idx$ts, ncol(data.f)]
> ruf <- randomUniformForest( X = x.train, 
+                             Y = y.train,
+                             xtest = x.test, 
+                             ytest = y.test,
+                             mtry = 1, ntree = 300,
+                             threads = 2, 
+                             nodesize = 2
+                             )
为了易于计算，将标记 -1 1 已经转换成 1 2 ，并用于内部替换。
> print(ruf)
Call:
randomUniformForest.default(X = x.train, Y = y.train, xtest = x.test, 
    ytest = y.test, ntree = 300, mtry = 1, nodesize = 2, threads = 2)

Type of random uniform forest: Classification

                           paramsObject
ntree                               300
mtry                                  
nodesize                              2
maxnodes                            Inf
replace                            TRUE
bagging                           FALSE
depth                               Inf
depthcontrol                      FALSE
OOB                                TRUE
importance                         TRUE
subsamplerate                         1
classwt                           FALSE
classcutoff                       FALSE
oversampling                      FALSE
outputperturbationsampling        FALSE
targetclass                          -1
rebalancedsampling                FALSE
randomcombination                 FALSE
randomfeature                     FALSE
categorical variables             FALSE
featureselectionrule            entropy

Out-of-bag (OOB) evaluation
OOB estimate of error rate: 20.2%
OOB error rate bound (with 1% deviation): 21.26%

OOB confusion matrix:
          Reference
Prediction   -1    1 class.error
        -1 1066  280      0.2080
        1   254 1043      0.1958

OOB estimate of AUC: 0.798
OOB estimate of AUPR: 0.7191
OOB estimate of F1-score: 0.7962
OOB (adjusted) estimate of geometric mean: 0.7979 

Breiman's bounds
Expected prediction error (under approximatively balanced classes): 18.42%
Upper bound: 27.76%
Average correlation between trees: 0.0472 
Strength (margin): 0.4516 
Standard deviation of strength: 0.2379 

Test set
Error rate: 19.97%

Confusion matrix:
          Reference
Prediction  -1   1 class.error
        -1 541 145      0.2114
        1  119 517      0.1871

Area Under ROC Curve: 0.8003
Area Under Precision-Recall Curve: 0.7994
F1 score: 0.7966
Geometric mean: 0.8001 

我们将简单解释下这些内容的含义：

• 训练误差为（内部误差）1% ，方差 = 21.26%。
• Breiman’s bounds — 由Breiman (2001)提出的理论边界值。因为Random Uniform Forests继承了Random Forest的属性，在此他们都是适用的。对于分类来说给出2个预测误差边界，树之间的平均相关性，强度及强度标准差。
• 预期预测误差 = 18.42%。误差上限 = 27.76%。
• 测试误差 = 19.97% (外部误差)。（如果外部误差小于等于内部误差，并且比Breiman边界的上限值小， 那么很可能无需重新训练。）

让我们看下训练误差图表：

> plot(ruf)

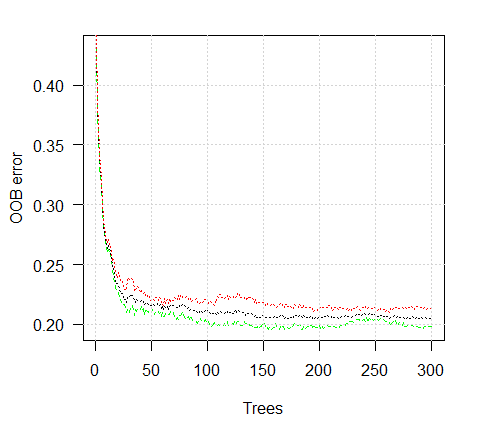
图 2. 训练误差取决于树的数量

现在我们考察预测因子的全局重要度。

> summary(ruf)

全局变量重要度：
注意：最具预测性的特征根据'score'排序并绘制。 
通过查看 'class'以及'class.frequency'，也必须把把最具判别能力的变量 
考虑在内。

   variables score class class.frequency percent
1        cci  2568     1            0.50  100.00
2     signal  2438     1            0.51   94.92
3      slowD  2437     1            0.51   94.90
4       oscK  2410     1            0.50   93.85
5        ADX  2400    -1            0.51   93.44
6        vol  2395     1            0.51   93.24
7        atr  2392    -1            0.51   93.15
8       sign  2388     1            0.50   92.97
9       vsig  2383     1            0.50   92.81
10        ar  2363    -1            0.51   92.01
11       chv  2327    -1            0.50   90.62
12       cmo  2318    -1            0.51   90.28
13        DX  2314     1            0.50   90.10
14     oscDX  2302    -1            0.51   89.64
15        tr  2217     1            0.52   86.31
   percent.importance
1                   7
2                   7
3                   7
4                   7
5                   7
6                   7
7                   7
8                   7
9                   7
10                  7
11                  7
12                  7
13                  6
14                  6
15                  6

Average tree size (number of nodes) summary:  
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
      3    1044    1313    1213    1524    1861 

Average Leaf nodes (number of terminal nodes) summary:  

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
      2     522     657     607     762     931 

Leaf nodes size (number of observations per leaf node) summary:  
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
   1.000    1.000    2.000    4.355    3.000 2632.000 

Average tree depth : 10 

Theoretical (balanced) tree depth : 11 

可见所有的输入参数都是显著并重要的。也就是说在那个分类中变量出现的最频繁。

更多的一些统计特征：

> pr.ruf <- predict(ruf, x.test, type = "response");
> ms.ruf <- model.stats(pr.ruf, y.test)
Test set
Error rate: 19.97%

Confusion matrix:
          Reference
Prediction  -1   1 class.error
        -1 540 144      0.2105
        1  120 518      0.1881

Area Under ROC Curve: 0.8003
Area Under Precision-Recall Curve: 0.7991
F1-score: 0.7969
Geometric mean: 0.8001 

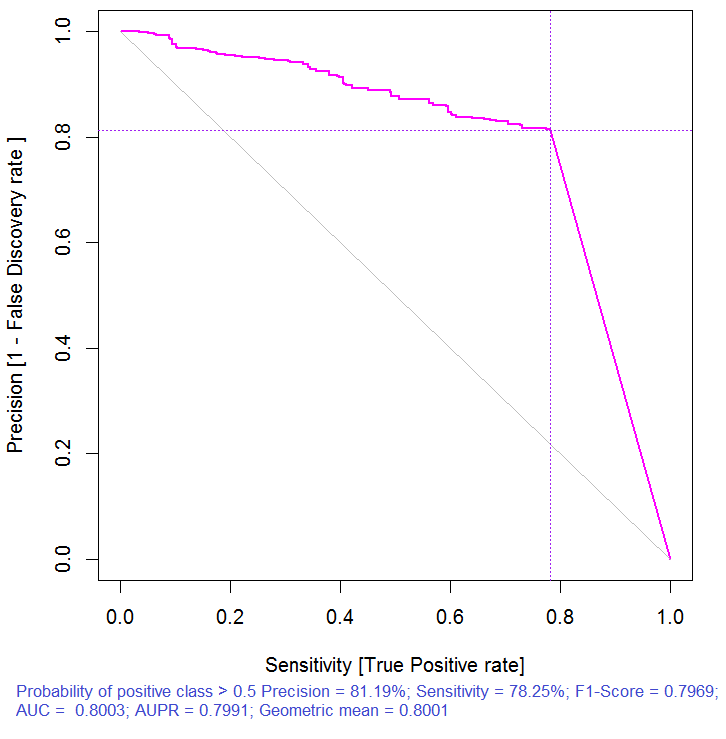
图 3. 精度回撤曲线

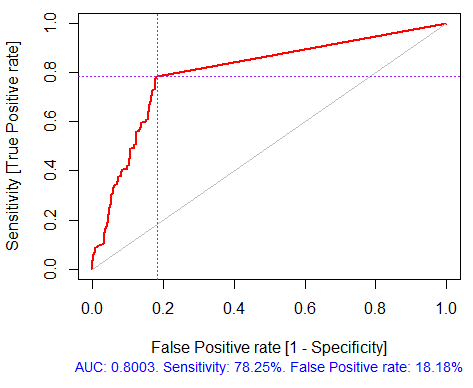
图 4. ROC曲线或误差曲线

如果像一般很多过滤器包中都提供的那样，我们就此打住，我们必须选择多个全局重要度最高的指标作为预测因子。这并不能带来良好的结果，因为没有考虑预测因子间的相互影响。

局部重要度

> imp.ruf <- importance(ruf, Xtest = x.test, maxInteractions = 3)

1 - 全局变量重要度 （15个基于信息增益的最重要变量）：
注意：最具预测性的特征根据'score'排序并绘制。 
通过查看 'class'以及'class.frequency'，也必须把把最具判别能力的变量 
考虑在内。

   variables score class class.frequency percent
1        cci  2568     1            0.50  100.00
2     signal  2438     1            0.51   94.92
3      slowD  2437     1            0.51   94.90
4       oscK  2410     1            0.50   93.85
5        ADX  2400    -1            0.51   93.44
6        vol  2395     1            0.51   93.24
7        atr  2392    -1            0.51   93.15
8       sign  2388     1            0.50   92.97
9       vsig  2383     1            0.50   92.81
10        ar  2363    -1            0.51   92.01
11       chv  2327    -1            0.50   90.62
12       cmo  2318    -1            0.51   90.28
13        DX  2314     1            0.50   90.10
14     oscDX  2302    -1            0.51   89.64
15        tr  2217     1            0.52   86.31
   percent.importance
1                   7
2                   7
3                   7
4                   7
5                   7
6                   7
7                   7
8                   7
9                   7
10                  7
11                  7
12                  7
13                  6
14                  6
15                  6


2 - 局部变量重要度
变量间的相互作用（10个一阶和二阶最重要的变量）：
对于每一个变量（每个顺序上），它同其他变量的相互影响被计算出来。

                cci    cmo  slowD   oscK signal    atr    chv
cmo          0.1933 0.1893 0.1345 0.1261 0.1146 0.1088 0.1062
cci          0.1770 0.1730 0.1182 0.1098 0.0983 0.0925 0.0899
slowD        0.1615 0.1575 0.1027 0.0943 0.0828 0.0770 0.0744
signal       0.1570 0.1530 0.0981 0.0897 0.0782 0.0725 0.0698
atr          0.1490 0.1450 0.0902 0.0818 0.0703 0.0646 0.0619
ADX          0.1468 0.1428 0.0879 0.0795 0.0680 0.0623 0.0596
ar           0.1452 0.1413 0.0864 0.0780 0.0665 0.0608 0.0581
oscK         0.1441 0.1401 0.0853 0.0769 0.0654 0.0596 0.0570
DX           0.1407 0.1367 0.0819 0.0735 0.0620 0.0562 0.0536
oscDX        0.1396 0.1356 0.0807 0.0723 0.0608 0.0551 0.0524
avg1rstOrder 0.1483 0.1443 0.0895 0.0811 0.0696 0.0638 0.0612
                ADX     tr     ar   vsig     DX  oscDX   sign
cmo          0.1026 0.1022 0.1013 0.1000 0.0977 0.0973 0.0964
cci          0.0864 0.0859 0.0850 0.0837 0.0815 0.0810 0.0802
slowD        0.0708 0.0704 0.0695 0.0682 0.0660 0.0655 0.0647
signal       0.0663 0.0659 0.0650 0.0637 0.0614 0.0610 0.0601
atr          0.0584 0.0579 0.0570 0.0557 0.0535 0.0531 0.0522
ADX          0.0561 0.0557 0.0548 0.0534 0.0512 0.0508 0.0499
ar           0.0546 0.0541 0.0533 0.0519 0.0497 0.0493 0.0484
oscK         0.0534 0.0530 0.0521 0.0508 0.0486 0.0481 0.0473
DX           0.0500 0.0496 0.0487 0.0474 0.0452 0.0447 0.0439
oscDX        0.0489 0.0485 0.0476 0.0463 0.0440 0.0436 0.0427
avg1rstOrder 0.0577 0.0572 0.0563 0.0550 0.0528 0.0524 0.0515
                vol avg2ndOrder
cmo          0.0889      0.1173
cci          0.0726      0.1010
slowD        0.0571      0.0855
signal       0.0526      0.0810
atr          0.0447      0.0730
ADX          0.0424      0.0707
ar           0.0409      0.0692
oscK         0.0397      0.0681
DX           0.0363      0.0647
oscDX        0.0352      0.0636
avg1rstOrder 0.0439      0.0000


基于相互作用的变量重要度（10个最重要的）：
   cmo    cci  slowD signal   oscK    atr    ADX     ar 
0.1447 0.1419 0.0877 0.0716 0.0674 0.0621 0.0563 0.0533 
   chv     DX 
0.0520 0.0485 

分类标签上的变量重要度 （10个最重要的变量 
的条件标签）：
       Class -1 Class 1
cci        0.16    0.23
cmo        0.20    0.18
slowD      0.09    0.10
oscK       0.09    0.07
signal     0.05    0.07
tr         0.02    0.07
ADX        0.06    0.03
chv        0.06    0.04
atr        0.05    0.06
ar         0.05    0.03

由此可见，基于相互影响的变量的重要度的前10名同全局重要度并不相符。最终，用于分类的变量重要度是考虑它们的贡献和影响在内的。请注意变量tr，基于全局重要度的话应该位于最后一位，理论上它应该被丢弃，但却因为强相互影响性使其排名升至第六位。

因此，前十位变量为：

> best <- Cs(cci, cmo,  slowD, oscK, signal, tr, ADX. chv, atr, ar)

让我们来验证下模型的质量是如何被最重要的预测因子改善的。

> x.tr <- x.train[ ,best]
> x.tst <- x.test[ ,best]
> ruf.opt <- randomUniformForest(X = x.tr,
+                                Y = y.train,
+                                xtest = x.tst, 
+                                ytest = y.test,
+                                ntree = 300, 
+                                mtry = "random",
+                                nodesize = 1,
+                                threads = 2)
为了易于计算，将标记 -1 1 已经转换成 1 2 ， 
并用于内部替换。
> ruf.opt
Call:
randomUniformForest.default(X = x.tr, Y = y.train, xtest = x.tst, 
    ytest = y.test, ntree = 300, mtry = "random", nodesize = 1, 
    threads = 2)

Type of random uniform forest: Classification

                           paramsObject
ntree                               300
mtry                             random
nodesize                              1
maxnodes                            Inf
replace                            TRUE
bagging                           FALSE
depth                               Inf
depthcontrol                      FALSE
OOB                                TRUE
importance                         TRUE
subsamplerate                         1
classwt                           FALSE
classcutoff                       FALSE
oversampling                      FALSE
outputperturbationsampling        FALSE
targetclass                          -1
rebalancedsampling                FALSE
randomcombination                 FALSE
randomfeature                     FALSE
categorical variables             FALSE
featureselectionrule            entropy

Out-of-bag (OOB) evaluation
OOB estimate of error rate: 18.69%
OOB error rate bound (with 1% deviation): 19.67%

OOB confusion matrix:
          Reference
Prediction   -1    1 class.error
        -1 1079  253      0.1899
        1   241 1070      0.1838

OOB estimate of AUC: 0.8131
OOB estimate of AUPR: 0.7381
OOB estimate of F1-score: 0.8125
OOB (adjusted) estimate of geometric mean: 0.8131 

Breiman's bounds
Expected prediction error (under approximatively balanced classes): 14.98%
Upper bound: 28.18%
Average correlation between trees: 0.0666 
Strength (margin): 0.5548 
Standard deviation of strength: 0.2945 

> pr.ruf.opt <- predict(ruf.opt, x.tst, type = "response")
> ms.ruf.opt <- model.stats(pr.ruf.opt, y.test)
Test set
Error rate: 17.55%

Confusion matrix:
          Reference
Prediction  -1   1 class.error
        -1 552 124      0.1834
        1  108 538      0.1672
Area Under ROC Curve: 0.8245
Area Under Precision-Recall Curve: 0.8212
F1-score: 0.8226
Geometric mean: 0.8244 

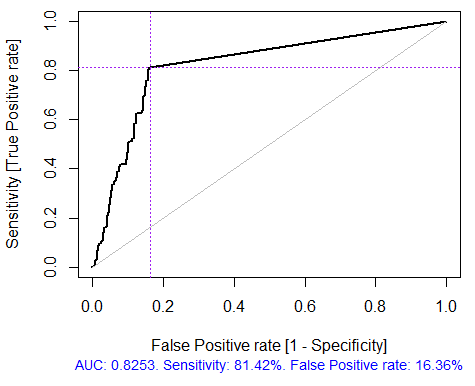
图. 5. ROC曲线或误差曲线

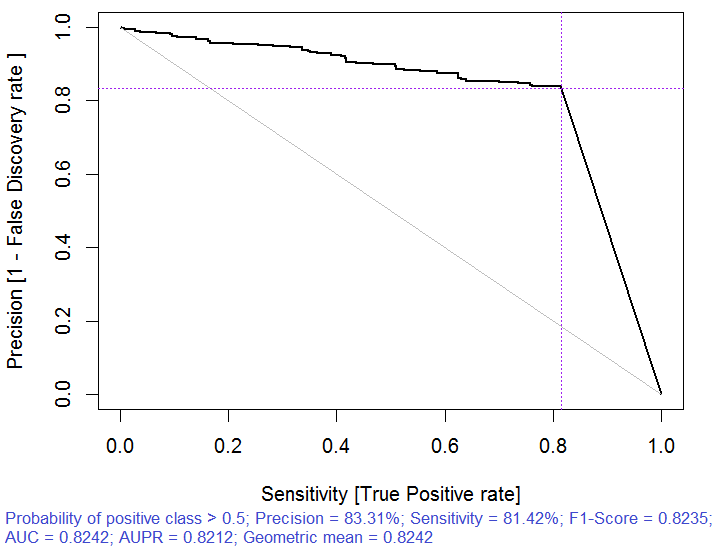
图. 6. 精度回撤曲线

模型质量显然得到了改善。测试集的预测误差为17.55%，比上限28.18%低，因此没有必要重新训练。模型还有很多其他参数，改变它们可能会进一步提升模型的质量，然而这不是本文当前的目标。

我们将继续探讨输入变量的最优数据集。

> imp.ruf.opt <- importance(ruf.opt, Xtest = x.tst)

 相关变量被提取出来。

1 - 全局变量重要度 （10个基于信息增益的最重要的变量）：
注意：最具预测性的特征根据'score'排序并绘制。 
通过查看 'class'以及'class.frequency'，也必须把把最具判别能力的变量 
考虑在内。

   variables score class class.frequency percent
1        atr  3556    -1            0.50  100.00
2       oscK  3487    -1            0.51   98.07
3        chv  3465     1            0.51   97.45
4     signal  3432     1            0.51   96.51
5        cci  3424     1            0.50   96.30
6      slowD  3415     1            0.51   96.04
7        ADX  3397    -1            0.50   95.52
8         ar  3369    -1            0.50   94.76
9         tr  3221     1            0.53   90.59
10       cmo  3177    -1            0.50   89.36
   percent.importance
1                  10
2                  10
3                  10
4                  10
5                  10
6                  10
7                  10
8                  10
9                   9
10                  9


2 - 局部变量重要度
变量间的相互作用（10个一阶和二阶最重要的变量）：
对于每一个变量（每个顺序上），它同其他变量的相互影响被计算出来。

                atr    cci   oscK  slowD    ADX     tr    chv
cci          0.1748 0.1625 0.1620 0.1439 0.1411 0.1373 0.1349
atr          0.1650 0.1526 0.1522 0.1341 0.1312 0.1274 0.1251
oscK         0.1586 0.1462 0.1457 0.1277 0.1248 0.1210 0.1186
chv          0.1499 0.1375 0.1370 0.1190 0.1161 0.1123 0.1099
ar           0.1450 0.1326 0.1321 0.1140 0.1112 0.1074 0.1050
signal       0.1423 0.1300 0.1295 0.1114 0.1085 0.1047 0.1024
ADX          0.1397 0.1273 0.1268 0.1088 0.1059 0.1021 0.0997
slowD        0.1385 0.1262 0.1257 0.1076 0.1048 0.1010 0.0986
cmo          0.1276 0.1152 0.1147 0.0967 0.0938 0.0900 0.0876
tr           0.1242 0.1118 0.1113 0.0932 0.0904 0.0866 0.0842
avg1rstOrder 0.1466 0.1342 0.1337 0.1156 0.1128 0.1090 0.1066
             signal     ar    cmo avg2ndOrder
cci          0.1282 0.1182 0.1087      0.1412
atr          0.1184 0.1084 0.0989      0.1313
oscK         0.1120 0.1020 0.0925      0.1249
chv          0.1033 0.0933 0.0838      0.1162
ar           0.0984 0.0884 0.0789      0.1113
signal       0.0957 0.0857 0.0762      0.1086
ADX          0.0931 0.0831 0.0736      0.1060
slowD        0.0919 0.0819 0.0724      0.1049
cmo          0.0810 0.0710 0.0615      0.0939
tr           0.0776 0.0676 0.0581      0.0905
avg1rstOrder 0.0999 0.0900 0.0804      0.0000


基于相互作用的变量重要度（10个最重要的）：
   atr    cci   oscK    chv  slowD    ADX signal     ar 
0.1341 0.1335 0.1218 0.0978 0.0955 0.0952 0.0898 0.0849 
    tr    cmo 
0.0802 0.0672 

分类标签上的变量重要度 
（10个针对每个标签的最重要变量）：
       Class -1 Class 1
atr        0.17    0.14
oscK       0.16    0.11
tr         0.03    0.16
cci        0.14    0.13
slowD      0.12    0.09
ADX        0.10    0.10
chv        0.08    0.10
signal     0.09    0.07
cmo        0.07    0.03
ar         0.06    0.06

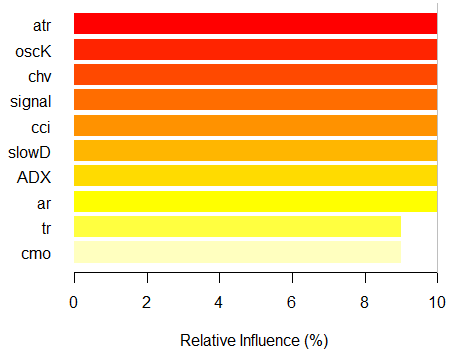
图. 7. 基于信息增益的变量重要度

如我们所见，全局变量重要度几乎已经趋于稳定，但是分类变量的重要度 排名有所不同。tr 变量位于第三位。

预测因子的部分依赖

那些重要度最高的变量的部分依赖将被考虑。

> plot(imp.ruf.opt, Xtest = x.tst)

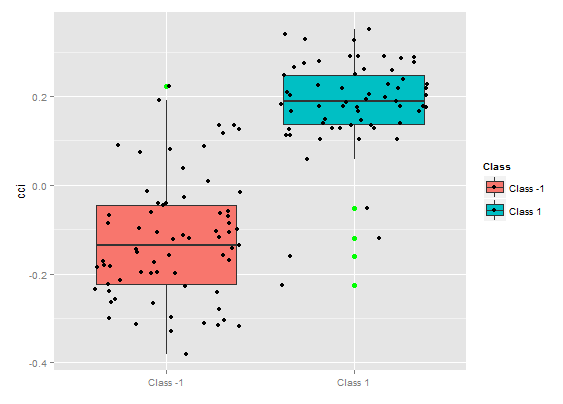
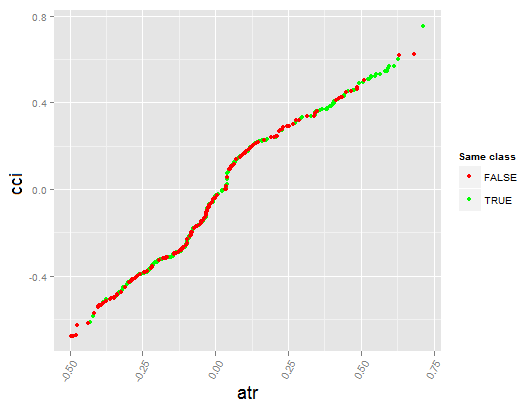
图. 8. cci变量的部分依赖性

上图显示了预测椅子cci的部分依赖性。分类之间的预测数据分割除了覆盖范围外，相对来说还不错。

> pd.signal <- partialDependenceOverResponses(x.tst,
+                                            imp.ruf.opt,
+                                            whichFeature = "signal",
+                                            whichOrder = "all"
+ )

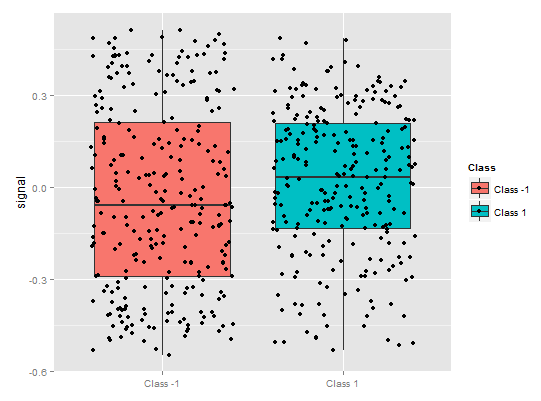
图. 9. signal变量的部分依赖性

上图中的预测因子signal的部分依赖性图形完全不同 。两个分类的几乎所有数据都在考察范围内。

> pd.tr <- partialDependenceOverResponses(x.tst,
                                          imp.ruf.opt, 
                                          whichFeature = "tr", 
                                          whichOrder = "all"
                                          )

预测因子tr的部分依赖性显示了分类的合理分割，并且仍旧具有相当的覆盖性。

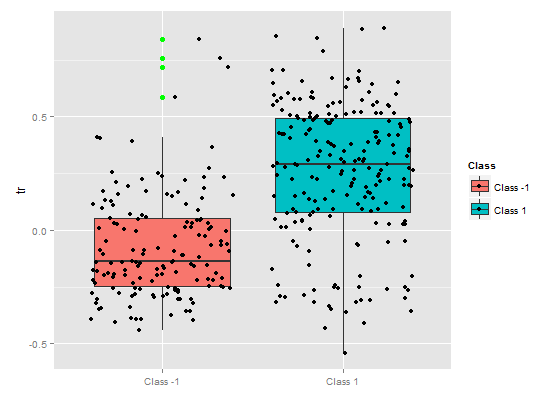
图. 10. tr变量的部分依赖性

> pd.chv <- partialDependenceOverResponses(x.tst,      
                                           imp.ruf.opt, 
                                           whichFeature = "chv", 
                                           whichOrder = "all")

chv预测因子的部分依赖性很差。观察分类的完整数据。

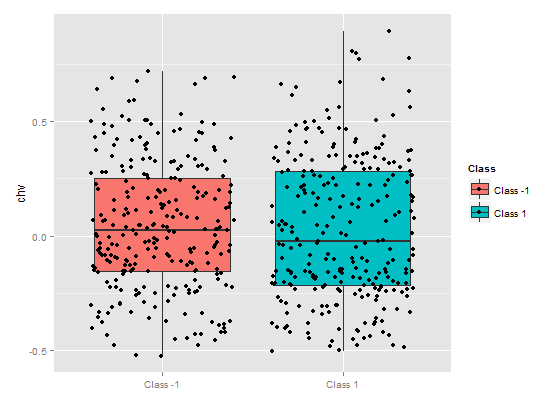
图. 11. chv变量的部分依赖性

用这种方式我们能够直观的确定预测因子数据是如何同分类联系起来以及如何将它们分隔开的。

分类的变量重要度

在分类上的“变量重要度”提供了一个局部视角：分类是固定的，意味着首先考虑重要的并且作为常量的变量来确定固定分类，最终，考虑针对每一分类的重要变量。因此，如果没有其他分类，则每一个变量都有重要度。

此处我们对能够选择确定分类的变量并不感兴趣，我们感兴趣的是当在做出选择时，在确定分类中有重要作用的变量。不考虑分类重要度，根据它们在每个分类中的排位，变量的顺序给出了其自由排名。

这个图表说明了些什么？tr预测因子对于类型“1”比类型“-1”重要很多。相反，预测因子oscK对于类型“-1”来说比类型“1”重要很多。<预测因子在不同的分类中的重要度也不同。

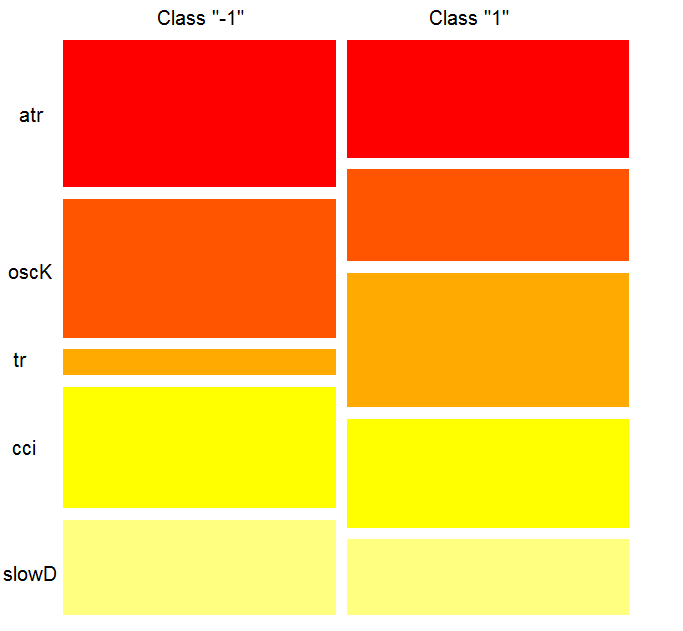
图. 12. 分类的变量重要度

基于相互影响的变量重要度

下图显示了每个变量的显示方式与任何其它变量的联合的相互作用。重要的一点提醒是：第一个变量并不一定是最重要的，而是对其他变量产生最大影响的。

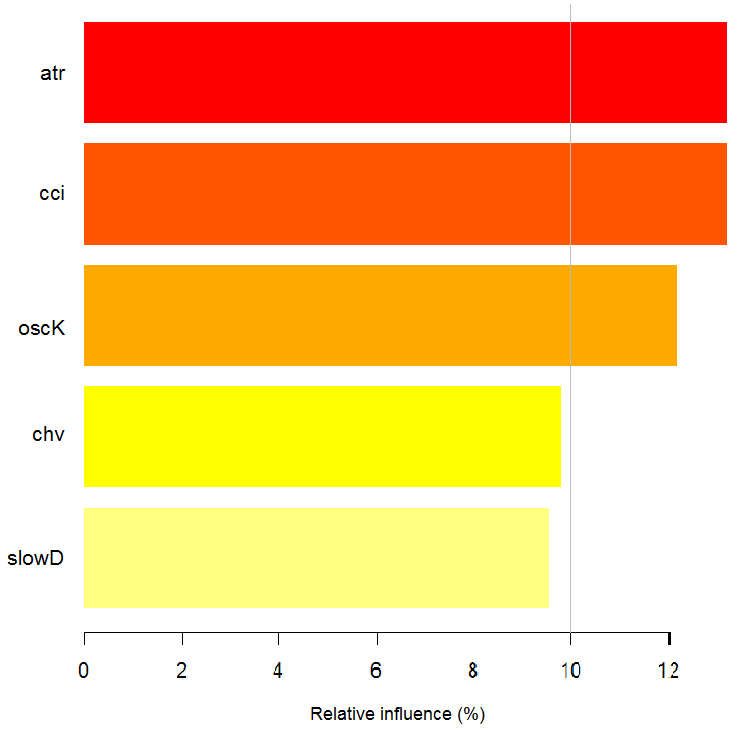
图.13. 基于相互影响的变量重要度

观察值上的变量互相影响情况

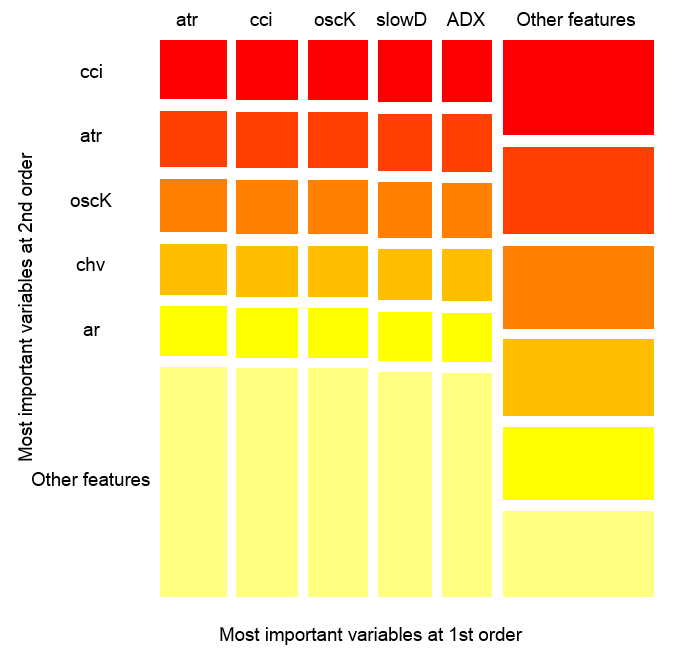
图. 14. 观察值上的变量重要度

上图显示了所有预测因子的一阶和二阶相互影响，相互作用的概念如我们之前的定义。它的面积为1。如果仅在考虑一个变量的基础上做出判定，一阶表示变量（降序排列）是最重要的。二阶表示，如果一个位置变量已经选择为第一顺序了，那么第二重要的变量就是那些在第二位的变量。

为了清晰起见，互相作用给出一个顺序特征表。首先给出最重要的变量。其次给出次重要的变量。从所有互相影响组合中给出一对变量之间的相互影响。请注意这取决于模型和数据两者。因此，模型的质量直接取决于预测的质量。我们也可以一个称为“other signs”的变量元，这样我们就可以让算法显示相对不重要的变量的默认试图。

部分重要度

你可以看看基于x.tst观测值的分类“-1”上的部分 重要度。

> par.imp.ruf <- partialImportance(X = x.tst, 
+                                  imp.ruf.opt, 
+                                  whichClass = "-1")
Relative influence: 67.41%
Based on x.tst  and class «-1»

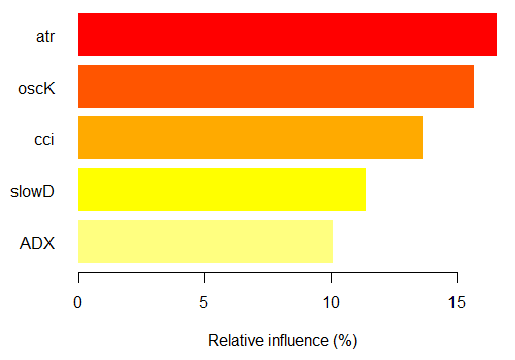
图. 15. 基于观测值的分类”-1″上的变量部分重要度

如我们所见，对应分类“-1”的五个最重要的预测因子如上图显示。

对于分类“+1”也同样

> par.imp.ruf <- partialImportance(X = x.tst, 
+                                  imp.ruf.opt, 
+                                  whichClass = "1")
Relative influence: 64.45%

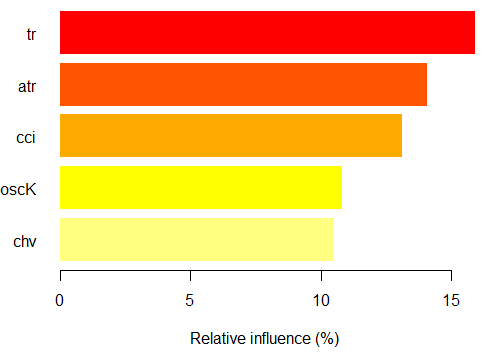
图. 16. 基于观测值的分类”+1″上的变量部分重要度

我们看到，预测因子在结构和排位方面都不同。

让我们看看预测因子 cci and atr, 的部分依赖性，它们是预测因子互相作用中最重要的一阶和二阶重要度。

> par.dep.1 <- partialDependenceBetweenPredictors(Xtest = x.tst,
+                             imp.ruf.opt,
+                             features = Cs(atr, cci),
+                             whichOrder = "all",
+                             perspective = T)

Level of interactions between atr and cci at first order: 0.1748
(99.97% of the feature(s) with maximum level)
Level of interactions between atr and cci at second order: 0.1526
(87.28% of the feature(s) with maximum level)

分类分布：对于一对中的一个变量，显示概率分布 
被考察的变量有同样的class。 
如果同样的class为 TRUE，那么这个变量很可能在预测时对其他变量 
有影响（对于当前的分类或者值）。

依赖性：对于变量对，显示它们的 
依赖关系，以及在 预测同一个class时针对定义依赖性的值 
的评估协议。对于分类变量， 
使用交叉制表。

热力图 ： 针对变量对，显示哪里的相关性 
是最强的。 
颜色越暗，相关性也越强。

在变量中，其决定作用的最可能是那个 
最具判断能力的（查看'全局变量重要度'） 
并/或那个具有高阶相互作用性的（查看 
'基于互相作用的变量重要度'）。

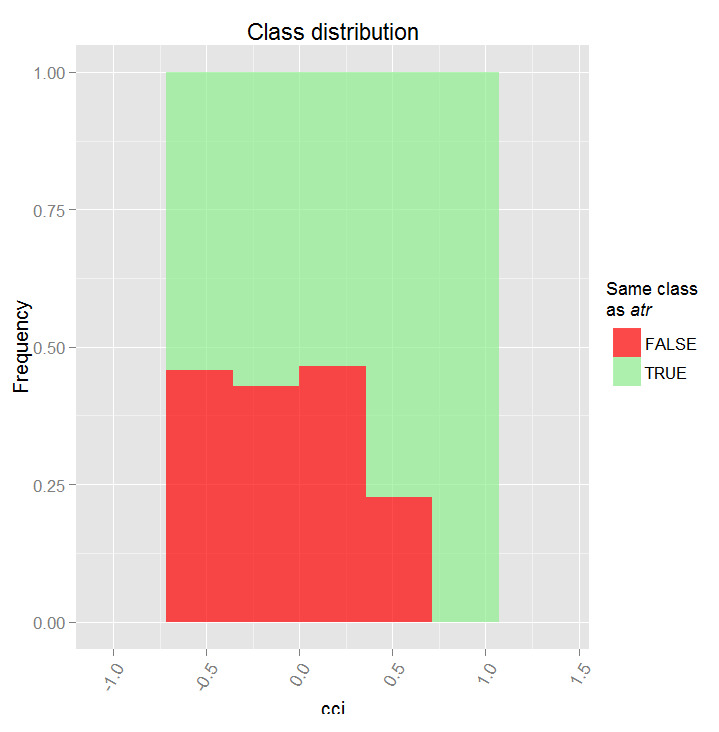
图. 17. 预测因子cci 和 atr之间的部分依赖性

图. 18. 预测因子atr 和 cci之间的依赖性

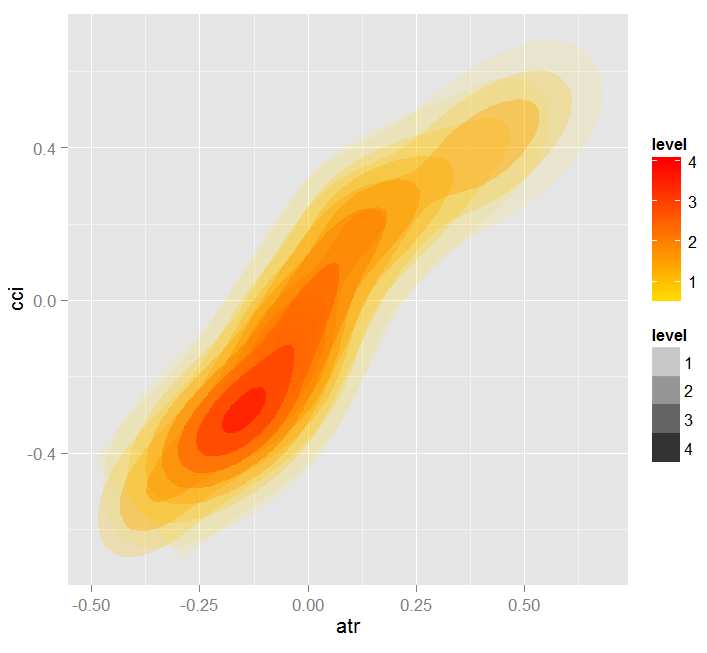
图. 19. 预测因子atr 和 cci依赖性之间的热力图

全局变量重要度用于确定哪个全局变量对于减小预测误差的作用最大。

局部变量重要度描述从变量相互影响角度来看，什么使得一个变量具有影响力。

这就产生了部分重要度的概念，它表示了何时一个变量更重要。分析变量重要度的最后一步是获得局部依赖性，设置一个变量是何时 以及/或者 如何同响应相关的。

总结：Random Uniform Forests中一个变量的重要度从最高到最低级别依次展开。首先，我们找出那些变量是重要的，学习每个分类的细微的差别。然后考虑到它们之间的相互作用，我们找到是什么使它们相互影响，并将所有的分类作为一个考虑后先选择一个变量。下一步 — 我们要知道当每种分类圈定的情况下它们的影响力从何而来。最后，通过观察“部分依赖性”，我们获知变量是何时以及如何被确认重要的。所有的步骤，除了”全局变量重要度“，都在任意训练或者测试集上进行操作。

已提出的多层次预测因子评估，通过显著降低数据维度和提升预测质量，来选择最重要的预测因子以及创建最优数据集。

你不仅可以评估和选择预测因子，还能够选择最具信息丰度的观测项。

让我们看看另一个有意思的包 — “RoughSet”。

Brief 描述到：这个包主要由两部分构成：Rough Set Theory (RST) 和 Fuzzy Rough Set Theory (FRST))。RST由 Z. Pawlak (1982, 1991)提出，它提供了一套复杂的数学工具用于建模和分析涵盖异质性和不确定性的信息系统。使用RST对象间不可分辨的关系不需要额外的参数来解析信息。

FRST理论，RST的扩展，由 D. Dubois 和 H. Prade (1990)提出，它将RST和由L.A.Zadeh (1965)在模糊理论中提出的不确定性和不可分辨性概念结合起来。这个概念使得你可以分析连续分布（变量）而无需预先将数据离散化。基于上述概念提出了许多方法并且已经应用到多个不同的领域中去了。为了解决问题，这个方法使用模糊关系和上下限的概念。

请允许我说些题外话。

信息表示的方法通常在信息系统中起了主要作用。在用归纳概念形成的系统中最著名的信息表示方法是：生产法则，决策树，谓词演算和语义网络。

为了解析和概括存储在实际信息阵列中的信息，会产生下述主要问题：

1. 数据是不一致的（定量，定质，结构）。
2. 真实的数据库通常很大，因此用于从数据库中检索信息的几何级复杂度的算法是不切实际的。
3. 包含在实际数据阵列中的信息可以是不完整的，过分的，扭曲的，有争议的并且许多属性的值可能完全缺失。因此，要构建分类规则你必须仅使用已经存在的属性。

目前，从数据库中提取信息（数据挖掘），粗糙集理论作为理论框架和一系列实用方法被越来越多的使用。

近似集没有确定的边界，例如，它们不能被可用属性集准确的描述出来。

近似集理论由 Zdzislaw Pawlak 在1982年提出并且成为处理不完整信息的新的数学工具。此理论最重要的概念是一个称为近似集的上下近似界限，可以通过“模糊”界限评估元素所属集的可能性或者必要性。

低阶近似由 完全属于X 的元素组成，高阶近似包含可能属于 X的元素。X集的边界范围是高和低阶近似不同之处，例如，具有X集的边界区域属于高阶近似而非低阶近似。

一个简单但功能强大的近似集的概念成为一个多理论 — 逻辑、基础代数、拓扑和应用研究，人工智能，近似推理，智能数据分析、决策理论、图像处理与模式识别的研究基础。

“近似集”的概念用于处理和信息的“粒度”相关的“数据缺失”。这个概念本质上是拓扑的并是用于处理其它知名的不完全信息方法的补充，如模糊集，贝叶斯推理、神经网络、进化算法、数据分析的统计方法。

让我们继续。所有在这个包中提供的方法被如下划分：

• RST 和 FRST的基本概念。在这一部分中我们可以观察四个不同的任务：不可分辨关系，上下近似，正域和差别矩阵。

• 离散化。它用于将物理数据转换成名称数据。以RST的角度来看，这是为了维持对象之间的差别。

• 特征选择这是一个发现预测因子子集的过程，试图保持同采用预测因子全集时一样的质量。换句话说就是为了选择基本特征并消除它们之间的依赖性。这在我们面对含有多重特征的数据集时是有用且必要的。对于RST和FRSt而言，预测因子选择就是对精简要素的搜寻。

• 示例选择。这个过程的目标是从训练数据集中移除噪声，不必要的或者冲突的副本。因此，通过去除不能给予模型正贡献的样本，来获取良好的分类精度。

• 规则归纳。如我们已经提到的，归纳法是为了生成规则，提供解决问题的相关知识。通常，在机器学习中这被称为训练。

• 预测/分类。这个任务的目标是从新的数据集中（测试集）预测变量的值。

我们仅研究此列表中的两项 — 预测因子的选择以及样本的选择。

让我们形成输入数据集和输出数据。我们将使用和之前获得的数据一样的数据，但将其转换到包所使用的“DecisionTable”类中。

> library(RoughSets)
加载所需的包： Rcpp
> require(magrittr)
> data.tr <- SF.asDecisionTable(data.f[idx$tr, ], 
+                               decision.attr = 16, 
+                               indx.nominal = 16)
> data.tst <- SF.asDecisionTable(data.f[idx$ts, ],
+                                decision.attr = 16, 
+                                indx.nominal = 16
+ )
> true.class <- data.tst[ ,ncol(data.tst)]

如前所述，RST使用标定数据。既然我们有的是连续的数值数据，我们将使用一个包中提供的特殊的离散化函数，来将其转换为标定数据。

> cut.values <- D.global.discernibility.heuristic.RST(data.tr)
> data.tr.d <- SF.applyDecTable(data.tr, cut.values)

让我们来看看结果：

> summary(data.tr.d)
           DX                ADX      
 (12.5,20.7]: 588   (17.6,19.4]: 300  
 (20.7, Inf]:1106   (19.4,25.4]: 601  
 [-Inf,12.5]: 948   (25.4,31.9]: 294  
                    (31.9, Inf]: 343  
                    [-Inf,17.6]:1104  
                                      
         oscDX                 ar     
 (1.81, Inf]:1502   (-40.6,40.6]:999  
 [-Inf,1.81]:1140   (40.6,71.9] :453  
                    (71.9, Inf] :377  
                    [-Inf,-40.6]:813  
                                      
                                      
                   tr                     atr      
 (0.000205,0.000365]:395   (0.00072,0.00123]:1077  
 (0.000365,0.0005]  :292   (0.00123, Inf]   : 277  
 (0.0005,0.00102]   :733   [-Inf,0.00072]   :1288  
 (0.00102,0.00196]  :489                           
 (0.00196, Inf]     :203                           
 [-Inf,0.000205]    :530                           
           cci                   chv      
 (-6.61, Inf]:1356   (-0.398,0.185]:1080  
 [-Inf,-6.61]:1286   (0.185,0.588] : 544  
                     (0.588, Inf]  : 511  
                     [-Inf,-0.398] : 507  
                                          
                                          
          cmo                sign     
 (5.81,54.1]: 930   [-Inf, Inf]:2642  
 (54.1, Inf]: 232                     
 [-Inf,5.81]:1480                     
                                      
                                      
                                      
            vsig              slowD     
 (0.0252, Inf]:1005   [-Inf, Inf]:2642  
 [-Inf,0.0252]:1637                     
                                        
                                        
                                        
                                        
                 oscK              signal    
 (-0.0403,0.000545]:633   (-11.4, Inf]:1499  
 (0.000545,0.033]  :493   [-Inf,-11.4]:1143  
 (0.033, Inf]      :824                      
 [-Inf,-0.0403]    :692                      
                                             
                                             
               vol      Class    
 (0.0055,0.00779]:394   -1:1319  
 (0.00779,0.0112]:756   1 :1323  
 (0.0112,0.0154] :671            
 (0.0154, Inf]   :670            
 [-Inf,0.0055]   :151  

我们看到预测因子被离散化成不同的值。像变量slowD, sign 完全没有被分离。变量signal, vsig, cci, oscDX被简单的分为两个区域。其他变量被分为3和6个分类。

我们选择重要的变量：

> reduct1 <- FS.quickreduct.RST(data.tr.d, control = list())
> best1 <- reduct1$reduct
> best1
    DX    ADX  oscDX     ar     tr    atr    cci 
     1      2      3      4      5      6      7 
   chv    cmo   vsig   oscK signal    vol 
     8      9     11     13     14     15 

没有被分离的数据 (slowD, sign) 从数据集中被移除。我们将执行测试集的离散化并且根据缩减执行情况进行变换。

> data.tst.d <- SF.applyDecTable(data.tst, cut.values)
> new.data.tr <- SF.applyDecTable(data.tr.d, reduct1)
> new.data.tst <- SF.applyDecTable(data.tst.d, reduct1)

现在，使用名为“induction rules”的包，我们将得到一系列绑定预测因子和目标的规则。下面的选项之一将被使用：

> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9, timesCovered = 3)

我们将在测试集上效验这些规则是如何用于预测的：

> pred.vals <- predict(rules, new.data.tst)
> table(pred.vals)
pred.vals
 -1   1 
655 667 

矩阵：

> caret::confusionMatrix(true.class, pred.vals[ ,1])
模糊矩阵及其统计数据

          Reference
Prediction  -1   1
        -1 497 163
        1  158 504
                                          
               Accuracy : 0.7572          
                 95% CI : (0.7331, 0.7801)
    No Information Rate : 0.5045          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.5144          
 Mcnemar's Test P-Value : 0.8233          
                                          
            Sensitivity : 0.7588          
            Specificity : 0.7556          
         Pos Pred Value : 0.7530          
         Neg Pred Value : 0.7613          
             Prevalence : 0.4955          
         Detection Rate : 0.3759          
   Detection Prevalence : 0.4992          
      Balanced Accuracy : 0.7572          
                                          
       'Positive' Class : -1  

现在 — 有意义样本的选择：

> ##-----Instance Selection-----------
> res.1 <- IS.FRIS.FRST(decision.table = data.tr, 
                        control = list(threshold.tau = 0.5, alpha = 1,
                        type.aggregation = c("t.tnorm", "lukasiewicz"),
                        t.implicator = "lukasiewicz"))
> new.data.tr <- SF.applyDecTable(data.tr, res.1)

> nrow(new.data.tr)
[1] 2353

大约300个样本被标记为无足轻重且可丢弃的。我们将从这个集从解析一系列规则，并将之与之前集的预测质量进行对比。

> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9, 
                          timesCovered = 3)
> pred.vals <- predict(rules, new.data.tst)
> table(pred.vals)
pred.vals
 -1   1 
638 684 
> caret::confusionMatrix(true.class, pred.vals[ ,1])
模糊矩阵及其统计数据

          Reference
Prediction  -1   1
        -1 506 154
        1  132 530
                                          
               Accuracy : 0.7837          
                 95% CI : (0.7605, 0.8056)
    No Information Rate : 0.5174          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.5673          
 Mcnemar's Test P-Value : 0.2143          
                                          
            Sensitivity : 0.7931          
            Specificity : 0.7749          
         Pos Pred Value : 0.7667          
         Neg Pred Value : 0.8006          
             Prevalence : 0.4826          
         Detection Rate : 0.3828          
   Detection Prevalence : 0.4992          
      Balanced Accuracy : 0.7840          
                                          
       'Positive' Class : -1 

前一个的预测质量要更高一些。需要注意的是，在RandomUniformForests,的情况下，不可能在重复试验中获得可重复的结果。每一次新的加载都能给出一个略微不同的结果。

规则看上去是什么样的？我们来看看：

> head(rules)
[[1]]
[[1]]$idx
[1]  6  4 11

[[1]]$values
[1] "(85.1, Inf]"    "(0.00137, Inf]" "(0.0374, Inf]" 

[[1]]$consequent
[1] "1"

[[1]]$support
 [1] 1335 1349 1363 1368 1372 1390 1407 1424 1449 1454
[11] 1461 1472 1533 1546 1588 1590 1600 1625 1630 1661
[21] 1667 1704 1720 1742 1771 1777 1816 1835 1851 1877
[31] 1883 1903 1907 1912 1913 1920 1933 1946 1955 1981
[41] 1982 1998 2002 2039 2040 2099 2107 2126 2128 2191
[51] 2195 2254 2272 2298 2301 2326 2355 2356 2369 2396
[61] 2472 2489 2497 2531 2564 2583 2602 2643

[[1]]$laplace
        1 
0.9857143 

列表中的数据如下：

1. $idx — 参与此规则预算的预测因子。这个例子中为 6(“atr”) , 4(“ar”) 和 11(“vsig”).
2. $values — 运行规则的指标值范围。
3. $consequent — 解：class = “1”。为了易于理解：如果“atr” 在范围“(85.1, Inf]”内并且“ar” 在范围“(0.00137, Inf]” 内并且“vsig” 在范围“(0.0374, Inf]”内，那么Class = “1”。
4. $support — 支持这一结论的样本索引。
5. $laplace — 这个规则的置信区间。

规则的计算需要相当多的时间。

总结

我们研究了基于预测因子评估、可视化以及选择最有价值预测因子的新方法。我们还探讨了不同的重要度等级，预测因子相关性以及它们对结果的影响。实验的结果将被应用于下一篇文章，在那里我们将研究RBM深度神经网络。