导言
货币和股票价格的图表总是包含价格波动, 其频率和幅度有所不同。我们的任务是判断基于这些短期和长期走势的主要趋势。一些交易者在图表上绘制趋势线, 而另一些人则使用指标。在这两种情况下, 我们的目的是将真正的价格走势从受到次要因素影响而导致的噪音中分离出来, 因为噪音只会产生短期效果。在本文中, 我提议利用卡尔曼滤波器将主要走势与市场噪音分开。
在交易中使用数字滤波器的思路并不鲜见。例如, 我曾 描述过 运用低通滤波器。但追求完美是无止境的, 所以我们再考察一个策略, 比较一下结果。
1. 卡尔曼滤波器原理
那么, 什么是卡尔曼滤波器, 为什么我们感兴趣呢?以下过滤器定义来自 维基百科 :
卡尔曼滤波器 是一种使用一系列随时间观测到的测量值的算法, 包含统计噪声和其它不准确性。
这意味着该滤波器最初是为处理噪声数据而设计的。还有, 它能够处理不完整的数据。另一个优点, 它是为动态系统设计并应用的; 我们的价格图表恰好属于这样的系统。
滤波器算法的工作在两个步骤中处理:
- 外推 (预测)
- 更新 (校正)
1.1. 外推, 系统数值的预测
滤波器操作算法的第一阶段是利用已分析过程的基础模型。在此模型基础上, 形成单步前瞻预测。
![]() (1.1)
(1.1)
其中:
- xk 是动态系统在第 k 步的外推值,
- Fk 是状态转换模型, 展体现当前系统状态对先前状态的依赖性,
- x^k-1 是系统的前一个状态 (前一步中的滤波值),
- Bk 是控制输入模型, 展现控制对系统的影响,
- uk 是系统上的控制向量。
例如, 控制效果可以是新闻因素。不过, 实际当中效果是未知的, 且被忽略, 而其影响是指噪声。
之后预测系统的协方差误差:
![]() (1.2)
(1.2)
其中:
- Pk 是动态系统状态向量的外推协方差矩阵,
- Fk 是状态转换模型, 展体现当前系统状态对先前状态的依赖性,
- P^k-1 是状态向量的协方差矩阵在前一步的更新,
- Qk 是过程的协方差噪声矩阵。
1.2. 系统值的更新
滤波器算法的第二步从测量实际系统的状态 zk 开始。考虑到真实系统状态和测量误差, 指定系统状态的实际测量值。在我们的案例中, 测量误差是噪声对动态系统的影响。
此刻, 我们已有两个不同的数值代表单个动态过程的状态。它们包括第一步计算的动态系统外推值, 和实际的测量值。这些具有一定的几率度的数值, 当中的每一个均表征我们过程的真实状态, 因此, 该值介于这两个值之间。因此, 我们的目标是确定信任度, 即此值或彼值的信任程度。为此目的, 执行卡尔曼滤波器第二阶段的迭代。
利用已有数据, 我们判断实际系统状态自外推值的偏差。
![]() (2.1)
(2.1)
此处:
- yk 是外推之后系统实际状态在第 k 步的偏差,
- zk 是第 k 步中系统的实际状态,
- Hk 是显示实际系统状态对于所计算数据依赖性的测量矩阵 (在实际中经常取值一),
- xk 是动态系统在第 k 步的外推值。
在下一步中, 计算误差向量的协方差矩阵:
![]() (2.2)
(2.2)
此处:
- Sk 是在第 k 步的误差矢量的协方差矩阵,
- Hk 是显示实际系统状态对于计算数据依赖性的测量矩阵,
- Pk 是动态系统状态向量的外推协方差矩阵,
- Rk 是测量噪声的协方差矩阵。
然后检测优化增益。增益反映了计算值和经验值的置信度。
![]() (2.3)
(2.3)
此处:
- Kk 是卡尔曼增益值的矩阵,
- Pk 是动态系统状态向量的外推协方差矩阵,
- Hk 是显示实际系统状态对于计算数据依赖性的测量矩阵,
- Sk 是在第 k 步的误差矢量的协方差矩阵。
现在, 我们使用卡尔曼增益来更新系统状态值和状态向量的协方差矩阵估值。
![]() (2.4)
(2.4)
其中:
- x^k 和 x^k-1 在在第 k 和 k-1 步的更新值,
- Kk 是卡尔曼增益值的矩阵,
- yk 是外推后在第 k 步的系统实际状态的偏差。
![]() (2.5)
(2.5)
其中:
- P^k 是更新后的动态系统状态向量的协方差矩阵,
- I 是标识符矩阵,
- Kk 是卡尔曼增益值的矩阵,
- Hk 是显示实际系统状态对于计算数据依赖性的测量矩阵,
- Pk 是外推的动态系统状态向量的协方差矩阵。
以上所有可以概括为以下规划
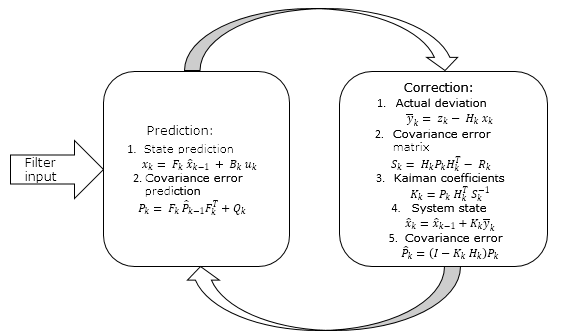
2. 卡尔曼滤波器的实现
现在, 我们已知晓了卡尔曼滤波器的工作原理。我们进入到实际实现。以上滤波器公式的矩阵形式允许接收若干个来源的数据。我建议在柱线收盘价基础上构建一个滤波器, 并将矩阵形式简化为离散的。
2.1. 输入数据初始化
在开始编写代码之前, 我们先定义输入数据。
如上所述, 卡尔曼滤波器的基础是一个动态过程模型, 用于预测过程的下一个状态。该滤波器最初旨在协同线性系统一起使用的, 其当前状态可轻易地通过前一状态乘以一个系数来定义。我们的情况有很更困难: 我们的动态系统是非线性的, 且比率在每一步都有变化。更甚的是, 我们不清楚该系统相邻状态之间的关系。这个任务似乎难以解决。这是一个棘手的解决方案: 我们将利用在这几篇文章中 [1],[2],[3] 描述的自回归模型。
我们开始吧。首先, 我们在这个类中声明 CKalman 类和所需的变量
class CKalman { private: //--- uint ci_HistoryBars; //用于分析的柱线数量 uint ci_Shift; //计算自回归的偏移 string cs_Symbol; //品名 ENUM_TIMEFRAMES ce_Timeframe; //时间帧 double cda_AR[]; //自回归系数 int ci_IP; //自回归系数的数量 datetime cdt_LastCalculated; //最后计算时间; bool cb_AR_Flag; //自回归计算的标志 //--- 卡尔曼滤波器的数值 double cd_X; // X double cda_F[]; // F 数组 double cd_P; // P double cd_Q; // Q double cd_y; // y double cd_S; // S double cd_R; // R double cd_K; // K public: CKalman(uint bars=6240, uint shift=0, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_H1); ~CKalman(); void Clear_AR_Flag(void) { cb_AR_Flag=false; } };
我们在类的初始化函数中为变量分配初值。
CKalman::CKalman(uint bars, uint shift, string symbol, ENUM_TIMEFRAMES period) { ci_HistoryBars = bars; cs_Symbol = (symbol==NULL ? _Symbol : symbol); ce_Timeframe = period; cb_AR_Flag = false; ci_Shift = shift; cd_P = 1; cd_K = 0.9; }
我使用了来自文章 [1] 的算法创建一个自回归模型。为此目的, 需要在类中添加两个私有函数。
bool Autoregression(void); bool LevinsonRecursion(const double &R[],double &A[],double &K[]);
LevinsonRecursion 函数按原样使用。Autoregression 函数有略微修改, 所以我们来仔细考察这个函数。在函数伊始, 我们检查分析所需的历史数据的可用性。如果没有足够的历史数据, 则返回 false。
bool CKalman::Autoregression(void) { //--- 检查数据不足 if(Bars(cs_Symbol,ce_Timeframe)<(int)ci_HistoryBars) return false;
现在, 我们加载所需的历史数据并填充实际状态转移模型系数的数组。
//--- double cda_QuotesCenter[]; //计算的数据 //--- 令所有价格可用 double close[]; int NumTS=CopyClose(cs_Symbol,ce_Timeframe,ci_Shift+1,ci_HistoryBars+1,close)-1; if(NumTS<=0) return false; ArraySetAsSeries(close,true); if(ArraySize(cda_QuotesCenter)!=NumTS) { if(ArrayResize(cda_QuotesCenter,NumTS)<NumTS) return false; } for(int i=0;i<NumTS;i++) cda_QuotesCenter[i]=close[i]/close[i+1]; // 计算系数
在准备操作之后, 我们检测自回归模型的系数个数, 并计算它们的值。
ci_IP=(int)MathRound(50*MathLog10(NumTS)); if(ci_IP>NumTS*0.7) ci_IP=(int)MathRound(NumTS*0.7); // 自回归模型的顺序 double cor[],tdat[]; if(ci_IP<=0 || ArrayResize(cor,ci_IP)<ci_IP || ArrayResize(cda_AR,ci_IP)<ci_IP || ArrayResize(tdat,ci_IP)<ci_IP) return false; double a=0; for(int i=0;i<NumTS;i++) a+=cda_QuotesCenter[i]*cda_QuotesCenter[i]; for(int i=1;i<=ci_IP;i++) { double c=0; for(int k=i;k<NumTS;k++) c+=cda_QuotesCenter[k]*cda_QuotesCenter[k-i]; cor[i-1]=c/a; // 自回归 } if(!LevinsonRecursion(cor,cda_AR,tdat)) // 莱文森-德宾 (Levinson-Durbin) 递归 return false;
现在我们将自回归系数的总和降低到 “1”, 并将计算执行的标志设置为 ‘true’。
double sum=0; for(int i=0;i<ci_IP;i++) { sum+=cda_AR[i]; } if(sum==0) return false; double k=1/sum; for(int i=0;i<ci_IP;i++) cda_AR[i]*=k;cb_AR_Flag=true;
接下来, 我们初始化滤波器所需的变量。为了计算噪声协方差, 我们使用所在分析周期的 Close 值的偏差的均方根值。
cd_R=MathStandardDeviation(close);
为了确定过程噪声协方差的值, 我们首先计算自回归模型值的数组, 并找出模型值的均方根偏差。
double auto_reg[]; ArrayResize(auto_reg,NumTS-ci_IP); for(int i=(NumTS-ci_IP)-2;i>=0;i--) { auto_reg[i]=0; for(int c=0;c<ci_IP;c++) { auto_reg[i]+=cda_AR[c]*cda_QuotesCenter[i+c]; } } cd_Q=MathStandardDeviation(auto_reg);
然后, 我们将实际的状态转换系数复制到 cda_F 数组, 从其可以进一步使用它们来计算新的系数。
ArrayFree(cda_F); if(ArrayResize(cda_F,(ci_IP+1))<=0) return false; ArrayCopy(cda_F,cda_QuotesCenter,0,NumTS-ci_IP,ci_IP+1);
对于我们系统的初始值, 我们使用的是最后 10 个值的算术平均值。
cd_X=MathMean(close,0,10);
2.2. 价格走势预测
在收到滤波器操作所需的所有初始数据之后, 我们可以继续进行实际实现。卡尔曼滤波器操作的第一步是 单步前瞻系统状态预测。我们创建一个 Forecast 公有函数, 在其内我们会实现函数 1.1 和 1.2。
double Forecast(void);
在函数伊始, 我们检查回归模型是否已经被计算。应在必要时调用其计算函数。在模型重新计算出错的情况下返回 EMPTY_VALUE,
double CKalman::Forecast() { if(!cb_AR_Flag) { ArrayFree(cda_AR); if(Autoregression()) { return EMPTY_VALUE; } }
之后, 我们计算状态转换系数并将其保存到 cda_F 数组的 “0” 单元中, 随后数值依次顺移一个单元。
Shift(cda_F); cda_F[0]=0; for(int i=0;i<ci_IP;i++) cda_F[0]+=cda_F[i+1]*cda_AR[i];
然后我们重新计算系统状态和出错概率。
cd_X=cd_X*cda_F[0]; cd_P=MathPow(cda_F[0],2)*cd_P+cd_Q;
该函数在最后返回预测的系统状态。在我们的情况中, 这是一根新柱线的预测收盘价。
return cd_X;
}
2.3. 校正系统状态
在下一个阶段, 在收到实际的柱线收盘价之后, 我们校正系统状态。为此目的, 我们来创建 Correction 公有函数。在函数参数中, 我们将传递实际的系统状态值, 即实际的柱线收盘价格。
double Correction(double z);
在该函数中实现了文章给出的 理论部分1.2。其完整代码可在附件中找到。在操作结束时, 该函数返回系统状态的更新 (校正) 值。
3. 卡尔曼滤波器的实际演示
我们来测试这个基于卡尔曼滤波器的类是如何工作的。我们创建一个基于这个类的指标。在新的蜡烛条开盘时, 指标调用系统更新函数, 然后调用函数来预测当前柱线的收盘价。类函数的调用顺序是相反的, 因为我们要为前一根收盘柱线调用更新 (校正) 函数, 再来预测当前的新柱线, 而其收盘价尚未得知。
指标有两个缓冲区。系统状态的预测值将被添加到第一个缓冲区之中, 更新的数值将被添加到第二个缓冲区中。我有意使用两个缓冲区, 令指标不会重绘, 我们可以看到系统在第二个滤波器的操作阶段是如何更新 (校正) 地。指标代码很简单, 可以在下面的附件中找到。这是指标操作的结果。
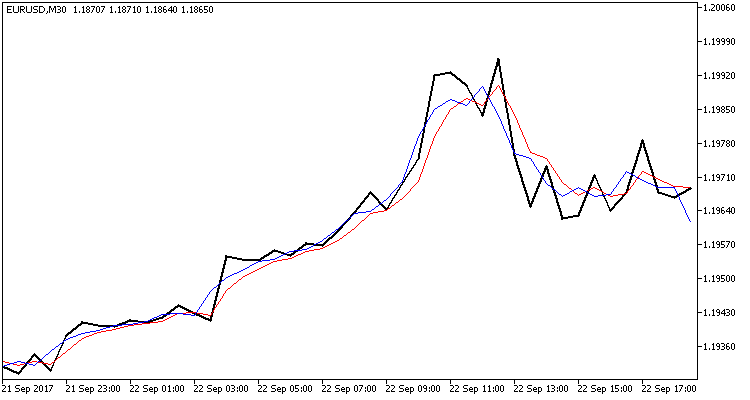
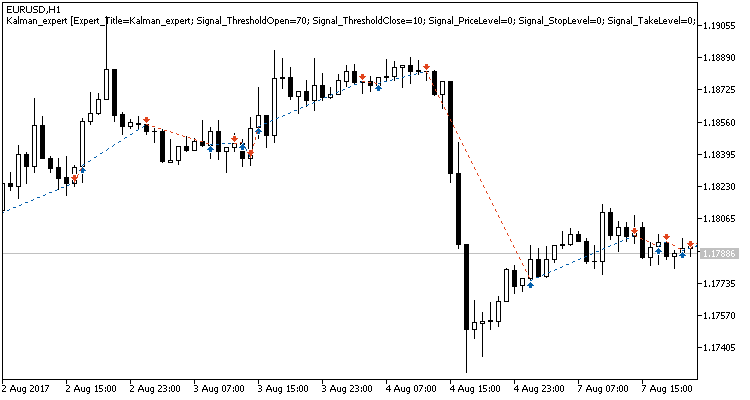
图表上显示三条虚线:
- 黑线显示实际的柱线收盘价
- 红线显示预测值
- 蓝线是由卡尔曼滤波器更新的系统状态
如您所见, 两条线都接近实际的收盘价, 且其显示的翻转点几率优良。请注意, 指标不会重绘, 并且在收盘价格尚不明了时, 红线在柱线开盘时即已绘制。
此图表显示了此滤波器的一致性, 以及利用此滤波器创建交易系统的可行性。
4. 利用 MQL5 向导创建交易信号模块
从上图我们可以看出, 红色系统状态预测线比黑色的实际价格折线更平滑。蓝线所示的矫正系统状态总在两者之间。换言之, 蓝线高于红线表示多头趋势。相反, 蓝线低于红线表示空头趋势。蓝线和红线的交汇点是趋势变化信号。
为了测试这个策略, 我们利用 MQL5 向导创建一个交易信号模块。交易信号模块的创建在本网站提供的多篇文章中均有描述: [1], [4], [5]。在此, 我将简要介绍一下与所描述的策略相关的要点。
首先, 我们创建 CSignalKalman 模块类, 它继承自 CExpertSignal。由于我们的策略基于卡尔曼滤波器, 我们需要在类中声明上面创建的 CKalman 类的一个实例。我们在模块中声明 CKalman 类实例, 所以它也会在模块中被初始化。出于这个原因, 我们需要将初始参数传递给模块。这就是上述任务在代码中是如何实现的:
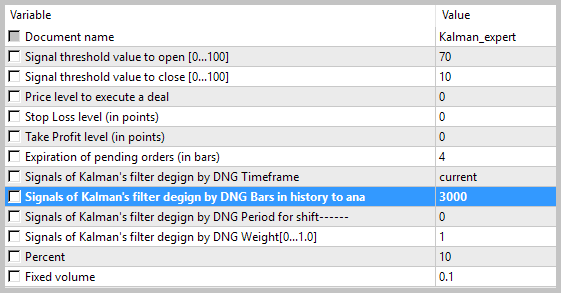
//+---------------------------------------------------------------------------+ // 向导描述开始 //+---------------------------------------------------------------------------+ //| 类描述 | //| 标题=Signals of Kalman's filter design by DNG | //| 类型=SignalAdvanced | //| 名称=Signals of Kalman's filter design by DNG | //| 简称=Kalman_Filter | //| 类=CSignalKalman | //| 主页=https://www.mql5.com/ru/articles/3886 | //| 参数=TimeFrame,ENUM_TIMEFRAMES,PERIOD_H1,Timeframe | //| 参数=HistoryBars,uint,3000,Bars in history to analysis | //| 参数=ShiftPeriod,uint,0,Period for shift | //+---------------------------------------------------------------------------+ // 向导描述结束 //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSignalKalman: public CExpertSignal { private: ENUM_TIMEFRAMES ce_Timeframe; //时间帧 uint ci_HistoryBars; //用于分析的历史柱线数量 uint ci_ShiftPeriod; //周期偏移 CKalman *Kalman; // 卡尔曼滤波器的类 //--- datetime cdt_LastCalcIndicators; double cd_forecast; // 预测值 double cd_corretion; // 校正值 //--- bool CalculateIndicators(void); public: CSignalKalman(); ~CSignalKalman(); //--- void TimeFrame(ENUM_TIMEFRAMES value); void HistoryBars(uint value); void ShiftPeriod(uint value); //--- 设置的验证方法 virtual bool ValidationSettings(void); //--- 创建指标和时间序列的方法 virtual bool InitIndicators(CIndicators *indicators); //--- 行情模型是否形成的检查方法 virtual int LongCondition(void); virtual int ShortCondition(void); };
在类初始化函数中, 我们将默认值分配给变量并初始化卡尔曼滤波器类。
CSignalKalman::CSignalKalman(void): ci_HistoryBars(3000), ci_ShiftPeriod(0), cdt_LastCalcIndicators(0) { ce_Timeframe=m_period; if(CheckPointer(m_symbol)!=POINTER_INVALID) Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe); }
在 CalculateIndicators 函数中使用滤波器计算系统状态。在函数的开始处, 我们需要检查滤波器数值在当前柱线上是否已计算过。如果这些值已被重新计算, 则退出该函数。
bool CSignalKalman::CalculateIndicators(void) { //--- 检查上次计算的时间 datetime current=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE); if(current==cdt_LastCalcIndicators) return true; // 如果数据已在此柱线上计算过, 则退出
然后检查最后的系统状态。如果未定义, 则重置 CKalman 类中的自回归模型计算标志 — 在这种情况下, 将在下一次类调用期间重新计算模型。
if(cd_corretion==QNaN) { if(CheckPointer(Kalman)==POINTER_INVALID) { Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe); if(CheckPointer(Kalman)==POINTER_INVALID) { return false; } } else Kalman.Clear_AR_Flag(); }
在下一步, 我们需要检查自上次函数调用以来出现了多少根柱线。如果间隔过大, 则重置自回归模型计算标志。
int shift=StartIndex(); int bars=Bars(m_symbol.Name(),ce_Timeframe,current,cdt_LastCalcIndicators); if(bars>(int)fmax(ci_ShiftPeriod,1)) { bars=(int)fmax(ci_ShiftPeriod,1); Kalman.Clear_AR_Flag(); }
然后重新计算所有未计算柱线的系统状态值。
double close[]; if(m_close.GetData(shift,bars+1,close)<=0) { return false; } for(uint i=bars;i>0;i--) { cd_forecast=Kalman.Forecast(); cd_corretion=Kalman.Correction(close[i]); }
重新计算后, 检查系统状态并保存最后的函数调用时间。如果操作已成功完成, 则该函数返回 true。
if(cd_forecast==EMPTY_VALUE || cd_forecast==0 || cd_corretion==EMPTY_VALUE || cd_corretion==0) return false; cdt_LastCalcIndicators=current; //--- return true; }
决策函数 (LongCondition 和 ShortCondition) 的结构完全相同, 只不过使用相反的交易开单条件。这是 ShortCondition 函数的代码示例。
首先, 我们启动滤波器数值重新计算函数。如果重新计算数值失败, 则退出该函数并返回 0。
int CSignalKalman::ShortCondition(void) { if(!CalculateIndicators()) return 0;
如果滤波器数值重新计算成功, 则将预测值与已更正的数值进行比较。如果预测值大于校正值, 则函数返回一个权重值。否则返回 0。
int result=0; //--- if(cd_corretion<cd_forecast) result=80; return result; }
该模块建立在 “反转” 原理上, 所以我们未实现平仓函数。
函数的所有代码都可以在文章所附的文件中找到。
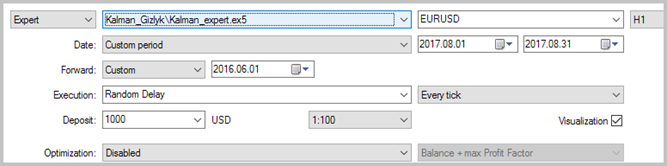
5. 智能交易系统测试
在文章 [1] 中详细描述了如何基于信号模块创建智能交易系统, 所以我们跳过这一步。请注意, 出于测试目的, EA 仅基于上面描述的一个 交易模块 并使用静态手数, 且不使用尾随止损。
智能交易系统的测试针对 EURUSD, 历史数据为 2017 年 8 月, 时间帧为 Н1。历史数据共有 3000 根柱线, 即接近 6 个月, 并用它们来计算自回归模型。EA 进行测试时, 没有止损和止盈, 以便观察卡尔曼滤波器对交易的明显影响。
测试结果显示有盈利交易占 49.33%。最高和平均盈利成交的利润超过相应的亏损交易的数额。一般来说, EA 测试在选定期限显现盈利, 盈利因子为 1.56。测试截图提供如下。
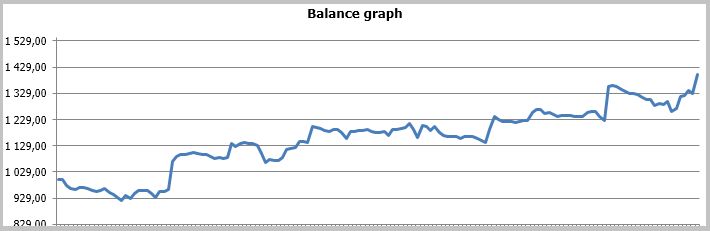
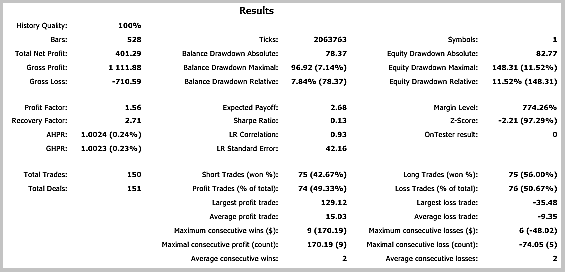
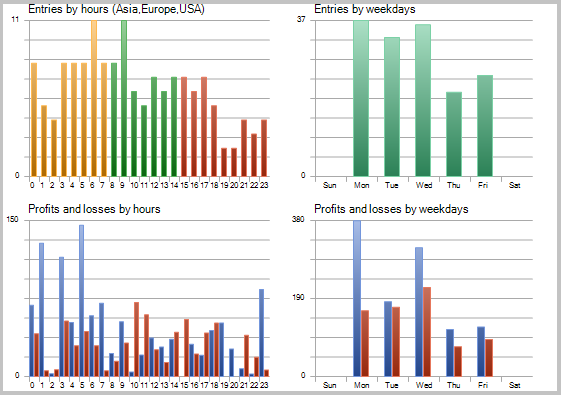
图表中的交易经过详细分析, 暴露出这种策略的两个缺陷:
- 在横盘走势当中有一连串亏损交易
- 开仓后稍晚即退出
当测试依据自适应行情追随 策略构建的 EA 时, 同样的问题也被暴露出来。在提及的文章中已推荐了解决这些问题的方案。然而, 与以前的策略不同, 基于卡尔曼滤波器的 EA 表现出正面的结果。在我看来, 本文提议并描述的策略如果辅以额外的判断横盘走势的滤波器, 则可以成功。利用时间滤波器可能会对结果有所改善。另一个改善结果的选项是增加持仓的退出信号, 以便防止盈利在急剧的反向走势中回吐。
结束语
我们已分析了卡尔曼滤波器的原理, 并在其基础上创建了一款指标和智能交易系统。测试表明, 这是一个有前途的策略, 且有助于暴露一些需要解决的瓶颈。
请注意, 本文仅提供一般信息和创建智能交易系统的示例, 这些在实际交易中绝非 “圣杯”。
我希望大家都能用严谨的方式进行交易, 并从交易中盈利!
URL 链接
- 自适应行情跟踪法的实际评估
- 时间序列的主要特征之分析
- AR 价格外推 – MetaTrader 5 的指标
- MQL5 向导: 如何创建一个交易信号模块
- 6 步创建您自己的交易机器人!
- MQL5 向导: 新版本
本文中使用的程序:
| # | 名称 | 类型 | 描述 |
|---|---|---|---|
| 1 | Kalman.mqh | 类库 | 卡尔曼滤波器类 |
| 2 | SignalKalman.mqh | 类库 | 卡尔曼滤波器基础上的交易信号模块 |
| 3 | Kalman_indy.mq5 | 指标 | 卡尔曼滤波器指标 |
| 4 | Kalman_expert.mq5 | 智能系统 | 利用卡尔曼滤波器的策略, 并据其构建智能交易系统 |
| 5 | Kalman_test.zip | 存档 | 该存档包含策略测试器中运行 EA 所获得的测试结果。 |
本文译自 MetaQuotes Software Corp. 撰写的俄文原文
原文地址: https://www.mql5.com/ru/articles/3886
MyFxtop迈投-靠谱的外汇跟单社区,免费跟随高手做交易!
免责声明:本文系转载自网络,如有侵犯,请联系我们立即删除,另:本文仅代表作者个人观点,与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。

 MyFxTops邁投財經
MyFxTops邁投財經
