内容
- 概述
- 1. 样品选择
- 2. 降维
- 2.1. 主分量分析 (PCA)
- 2.2. 独立分量分析 (ICA)
- 2.3. 概率主分量分析 (PPCA)
- 2.4. Autoencoder (非线性 PCA)
- 2.5. 逆向非线性 PCA (NLPCA)
- 3. 将数据集合划分为训练/验证/测试集合
- 结束语
- 应用
概述
这是描述数据准备的第三篇 (最后一篇) 文章 – 神经网络最重要的工作阶段。我们将研究两种非常重要的数据准备方法。它们正在消除噪音并降低输入维度。方法描述将附有详细的示例和图表。
1. 样品选择
噪音样本是指训练样本的错误标签。这是十分不寻常的数据特性。为了克服这个问题, 我们将使用 NoiseFilterR 软件包, 其中已实现了经典和现代噪声滤波器。
如今, 数据挖掘不得不面对日益复杂的数据问题。这不在于数据量, 而是它们的缺陷和不同形式, 给探险者们呈现出众多变幻场景。因此, 初步数据处理已成为 KDD (数据库中的知识发现) 流程的重要组成部分。与此同时, 开发用于初步数据处理的软件为工作提供了足够的工具。
初步数据处理需要以下算法才能从数据集合中提取最大信息。这是 KDD 整个过程中能量、时间消耗最多的阶段之一。初步数据处理可以分割为子任务。举例来说, 这可以是预测因子的选择或消除遗失及噪音数据。预测因子的选择目标是提取用于培训的最重要属性, 从而简化模型并减少计算时间。遗失数据的处理对于尽可能多地存储数据是必需的。噪音数据是不正确数据, 或是从数据分布中筛选出的数据。
所有这些问题都可由众多可选的软件来解决。举例来说, KEEL (RKEEL) 工具包含一组涵盖上述所有操作的初步数据处理算法。还有其它流行的解决方案, 如 WEKA (RWEKA), 或 RapidMiner 用于选择预测变量。还有一些独特的数据挖掘程序组合, 如 R, KNIME 或 Python。
对于统计软件 R, 综合 R 存档网络 (CRAN) 包含很多用于解决初步数据处理问题的软件包。
真实数据集合始终包含缺陷和噪音。这种噪音对分类器的训练有负面影响, 反过来又降低了预测精度, 使模型过度复杂化并增加了计算时间。
关于分类的指定文献区分了两种不同类型的噪音: 属性噪音和标签噪音 (或类噪音)。第一个是由于训练数据集合属性的缺陷而发生的, 第二个是由于分类方法中的错误而产生的。NoiseFiltersR 软件包主要关注标签噪音 – 最有害的标签噪音, 因为标签的质量对训练分类器非常重要。
此处描述了解决噪音标签问题的两个主要方法。您可关注近期 Benoit Frenay 和 Michel Verleysen 的工作 深入研究它们。
- 一方面, 通过创建不会受到噪音很大影响的可靠分类算法来解决问题, 这是算法级别的途径。这种情况下每个算法都将是一个特定的, 非通用的解决方案。
- 另一方面, 数据级别的方法 (过滤器) 是尝试开发清洁数据的策略, 这将在分类器的训练之前进行。NoiseFiltersR 软件包使用第二种方法。这是因为它仅允许初步数据处理一次, 之后分类器可以根据需要进行多次更改。
以下分类器具有抗噪声能力: С4.5, J48 和 Jrip (WEKA)。
我们来进行一些实验。我们来处理以下数据集合: DT (初步处理前的原始数据), DTn (仅常规化的原始数据集), DTTanh.n (无异常值, 三角变换和常规化) 和经 ORBoostFilter() 函数处理的训练集合, 函数是用于去除噪音的滤波器。我们看看经过这样的处理之后, 分布如何变化。
evalq({
#-----DT---------------------
out11 <- ORBoostFilter(Class~., data = DT$train, N = 10, useDecisionStump = TRUE)
DT$train_clean1 <- out11$cleanData
#----------DTTanh.n------------------------
out1 <- ORBoostFilter(Class~., data = DTTanh.n$train, N = 10, useDecisionStump = TRUE)
DTTanh.n$train_clean1 <- out1$cleanData
#-----------DTn--------------------------------
out12 <- ORBoostFilter(Class~., data = DTn$train, N = 10, useDecisionStump = TRUE)
DTn$train_clean1 <- out12$cleanData
},
env)
#---Ris1-----------------
require(funModeling)
evalq({
par(mfrow = c(1,3))
par(las = 1)
boxplot(DT$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DT$train_clean1")
boxplot(DTn$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DTn$train_clean1")
boxplot(DTTanh.n$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DTTanh.n$train_clean1")
par(mfrow = c(1,1))
}, env)
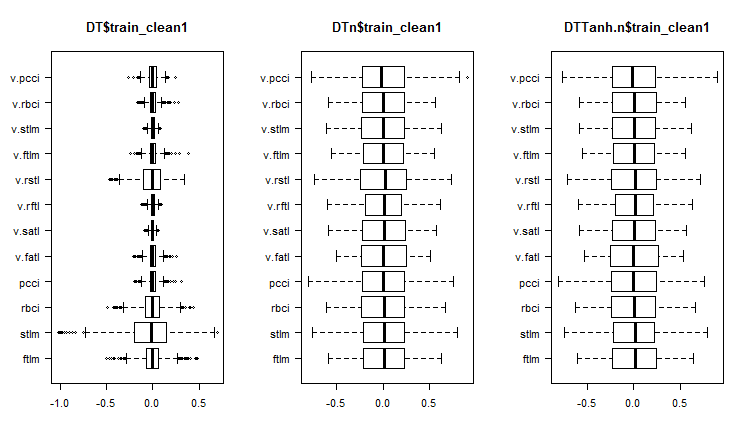
图例. 1. 去除噪声样本后的集合中预测因子的分布
我们看看这些集合中的变化和协方差是什么:
#----Ris2------------------ require(GGally) evalq(ggpairs(DT$train_clean1 %>% select(-Data), columns = c(1:6, 13), mapping = aes(color = Class), title = "DT$train_clean1/1"), env)
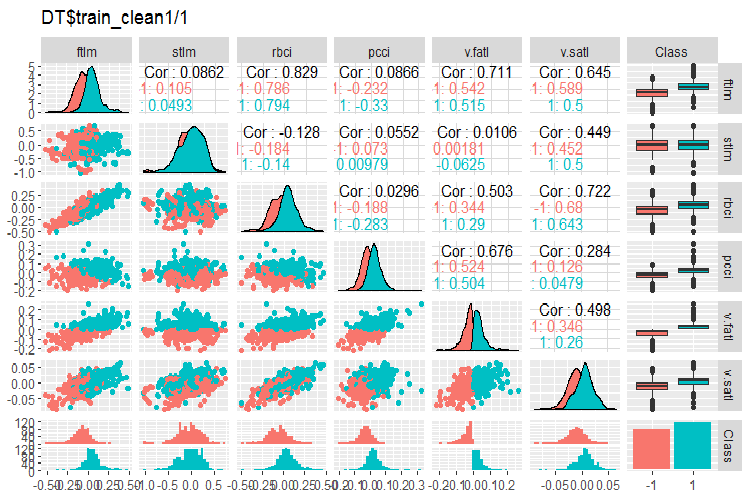
图例. 2. 删除噪声样本后 DT$train_clean1/1 中的变化和协方差
#-----Ris3--- evalq(ggpairs(DT$train_clean1 %>% select(-Data), columns = 7:13, mapping = aes(color = Class), title = "DT$train_clean1/2"), env)
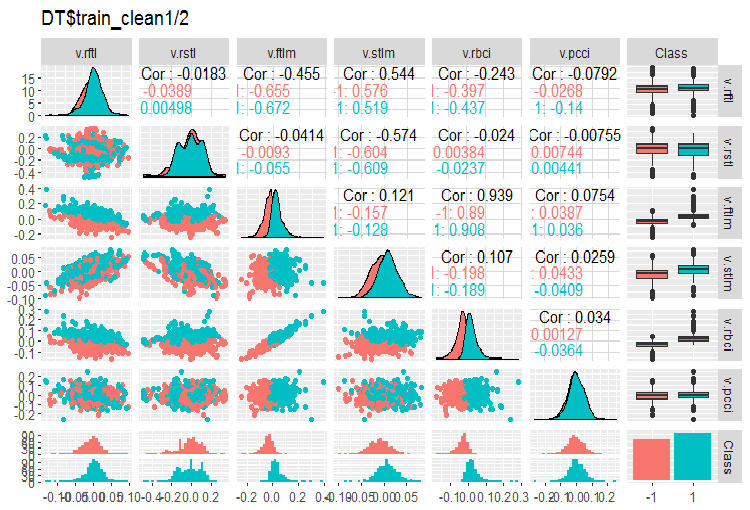
图例. 3. 删除噪声样本后 DT$train_clean1/2 中的变化和协方差
从 DT$train 集合中删除了多少样品?
> env$out11$remIdx %>% length()
[1] 658
大约 30% 左右。有两种方法可以解决。第一个是从训练集合中去除噪声样本, 并将其传递给模型进行训练。 第二个是用一个新的类标签重新排列, 并在完整的训练集合上训练模型, 但是增加一个目标变量。有了这样的噪音样本, 第二种情况看起来更有利。我们应该测试一下。
在无噪音的变量分布图上我们可以看到什么?
- 非常显着, 预测因子的分布通过目标变量进行划分。这有很大可能会显著提高我们正训练的模型的准确性。
- 几乎所有的异常值已被移除。
我们将使用过滤器清理 DTN$train DTTanh.n$train 数据集合。您会惊奇地发现, 在第一种情况下, 大量噪声变量也是如此。
c(env$out1$remIdx %>% length(), env$out12$remIdx %>% length())
[1] 652 653
这是否意味着没有能令噪声样本变得有用的变换?这值得测试一下。
我们来看看去除噪声变量后的 DTTanh.n$train 集合的变化和协方差。
#----Ris4----------------------- evalq(ggpairs(DTTanh.n$train_clean1, columns = 1:13, mapping = aes(color = Class), upper = "blank", title = "DTTanh.n$train_clean_all"), env)
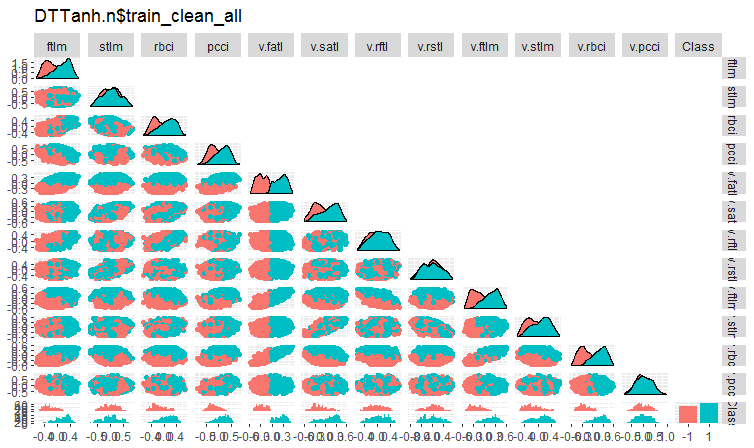
图例. 4. 删除噪声样本后 DTTanh.n$train_clean 集合中的变化和协方差。
所有带 v.fatl. 的变量的协方差非常有趣。我们可以直观地识别与目标变量无关的预测因子。它们是 stlm, v.rftl, v.rstl, v.pcci。我们将在另一集合上使用其它方法来测试这个假设。
对于 DTn$train_clean1 的相同图表:
#-------ris5---------- require(GGally) evalq(ggpairs(DTn$train_clean1 %>% select(-Data), columns = 1:13, mapping = aes(color = Class), upper = "blank", title = "DTn$train_clean1_all"), env)
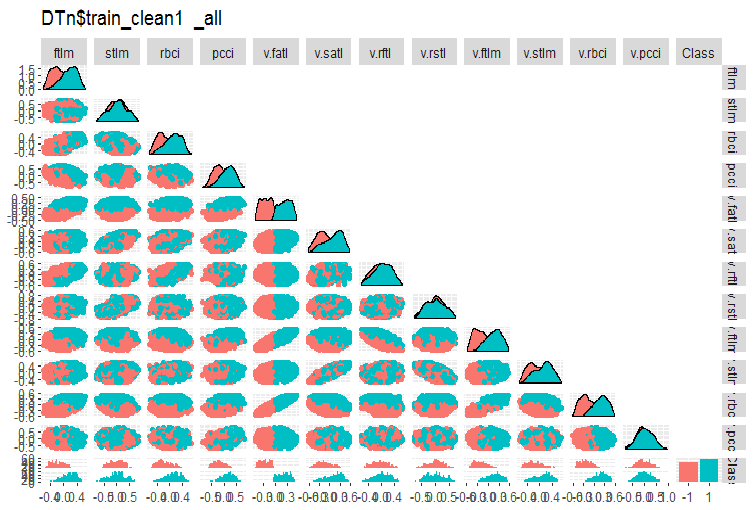
图例. 5. 删除噪声样本后 DTn$train_clean 中的变化和协方差。
在此我们可以看到, stlm, v.rftl, v.rstl, v.pcci 预测因子的变化不会被目标变量的等级分割。模型进行训练实验后, 由开发者决定如何处理噪声变量。
现在, 我们来看看在噪声样本被去除之后, 这些数据集合中预测因子的重要性如何发生变化。
#--------Ris6--------------------------- require(smbinning) par(mfrow = c(1,3)) evalq({ df <- renamepr(DT$train_clean1) %>% targ.int sumivt.dt = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.dt, cex = 0.8) rm(df) }, env) evalq({ df <- renamepr(DTTanh.n$train_clean1) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.8) rm(df) }, env) evalq({ df <- renamepr(DTn$train_clean1) %>% targ.int sumivt.dtn = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.dtn, cex = 0.8) rm(df) }, env) par(mfrow = c(1, 1))
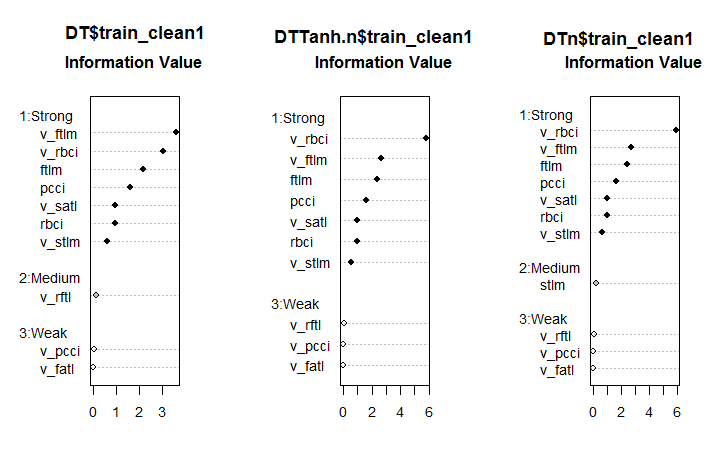
图例. 6. 在三个集合中的预测因子重要性
这是一个出乎意料的结果。v.fatal 变量证明是弱者中的最弱者!
在所有集合中七个强大的预测因子是相同的。中等强度的一个预测因子出现在第一和第三集合。经计算发现 stlm, v.rftl, v.rstl, v.pcci 预测因子确定为不相关, 这与较早的计算一致。所有这些计算都必须通过真实模型的实验来验证。
NoiseFilterR 软件包含有十几个用于识别噪声样本的其它滤波器。实验快乐!
2. 降维
降维是指将具有较大维度的初始数据变换成较小维度的新表示形式, 并保留主要信息。理想地, 变换表示的维度等于数据的内部维度。数据的内部维度是表示数据所有可能特征所需的最小变量数。传统上用于降低维度的算法: 主分量分析 (PCA), 独立分量分析 (ICA) 和奇异值分解 (SVD) 等等。.
降维能够软化所谓的维度诅咒和高维空间的其它不期望的特征。在描述数据的阶段, 它有以下目的。
- 它在数据处理期间降低了计算成本
- 减少重复训练的需求。特征越少, 数据中隐藏关系的可靠恢复所需的对象越少, 恢复这种关系的质量越好。
- 压缩数据以更有效地存储信息。在这种情况下, 随同 X → T 变换, 必须有机会进行逆变换 T → X
- 数据可视化。将样本投影到二维或三维空间能够以图形方式表示样本
- 提取新特征。在 X→ T 变换期间获得的新特征也许在以下识别解决方案的实现 (例如主分量分析) 期间可能产生重大影响,
请注意, 以下简述的所有降维方法属于无监督训练的类别。这意味着只有对象 X (预测因子) 的特征描述才起到初始信息的作用。
2.1. PCA, 主分量分析
(主分量分析, PCA) 是降低数据维度的最简单方法。这种方法的主要思想可追溯到 19 世纪。该方法的原理是在初始空间中找到设置维度的超平面, 并将数据集合投影到此超平面。选择投影数据误差最小的超平面 (方差之和)。
可由用户预设约化空间的维度 d。如果我们有可视化数据 (d = 2 或 d = 3), 或将数据集合放入一组存储器的问题, 则该值很容易选择。在其它情况下, 从先前的假设来看, d 的选择并不明显。
有一种简单的启发式方法来选择主分量方法的 d 值。主分量方法的一个特点是所有约化空间 d = 1, 2, . . . 彼此插入。这样一来, 一旦协方差矩阵的所有特征向量和特征值都被计算, 我们可以获得任意 d 值的约化空间。因此, 为了选择 d 值, 特征值可以按照递减的顺序显示在图表上, 并且可以设置截止阈值, 使得与零无关的值可以在右手侧。选择 d 值的另一种方法是选择阈值, 令曲线之下总面积的百分比保持在右侧 (例如 5% 或 1%)。
简单来说, 如果它们的数量很明显 (>50), PCA 可以作为噪音预测因子的初期抑制。
2.2. ICA, 独立分量分析
不像 PCA 那样, 独立分量分析 是最近的事情, 然而在各种数据探索领域迅速普及。
与主分量分析不同, ICA 变换需要一个模型。最常见的模型是假设 P 变量是从独立变量 p 的线性变换推导得来的。ICA 的目标是恢复初始的独立变量。大多数 ICA 算法首先启用数据白化, 然后以这种方式旋转数据, 使得所得到的分量尽可能独立。当分量按顺序构造时, 这意味着要搜索早前提到的未与预测相联的大型非高斯投影。
在信号处理期间, 独立分量的方法被广泛应用。这种技术将初始数据线性地转换成新的分量。新分量将尽可能地相互统计性独立。独立分量不必正交, 但它们的统计性独立比 PCA 中缺乏统计性相关更严格。
PCA 和 ICA 方法通过 preProcess() 函数在 caret 软件包中实现。在此函数中, 可以设置 PCA 覆盖的主分量数量或累积百分比。独立分量分析有两个阶段。首先, 在训练数据集合上计算所需参数。然后, 使用 predict() 转换数据集合和随后的所有新数据。
表 1. PCA 和 ICA 的比较特征
| 方法 | 优点 | 缺点 | 特点 | 大多数情况下获得的结果 | 计算新的主分量的方法 |
|---|---|---|---|---|---|
| PCA | 简单性 计算 |
|
解的非唯一性 (旋转不确定性)。每次基于一次训练测试的新计算都会产生不同的主分量。 |
|
Tnew = Xnew * P |
| ICA | 简单性计算 |
|
输入数据集合和独立分量的维度差异较大, 连续使用 PCA – > ICA。 |
|
Snew =scale( Xnew )* W * K |
我们进行实验。将脚本计算的结果从文章 Part_1.Rda 的第一部分加载到 Rstudio 中。以下是 env 的内容:
> ls(env) [1] "cap1" "cap2" "Close" "Data" "dataSet" [6] "dataSetCap" "dataSetClean" "dataSetOut" "High" "i" [11] "k" "k.cap" "k.out" "lof.x" "lof.x.cap" [16] "Low" "lower" "med" "Open" "out.ftlm" [21] "out.ftlm1" "pr" "pre.outl" "preProClean" "Rlof.x" [26] "Rlof.x.cap" "sk" "sk.cap" "sk.out" "test" [31] "test.out" "train" "train.out" "upper" "Volume" [36] "x" "x.cap" "x.out"
取含异常值插补的 x.cap 数据集合, 并使用 preProcess::caret 函数计算其主分量和独立分量。明确指定 PCA 和 ICA 的分量数量。我们不会指定 ICA 的常规化方式。
require(caret)
evalq({
prePCA <- preProcess(x.cap,
pcaComp = 5,
method = Hmisc::Cs(center, scale, pca))
preICA <- preProcess(x.cap,
n.comp = 3,
method = "ica")
}, env)
让我们来看一下变换的参数:
> str(env$prePCA) List of 20 $ dim : int [1:2] 7906 11 $ bc : NULL $ yj : NULL $ et : NULL $ invHyperbolicSine: NULL $ mean : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ std : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ ranges : NULL $ rotation : num [1:11, 1:5] -0.428 -0.091 -0.437 -0.107 -0.32 ... ..- attr(*, "dimnames")=List of 2 .. ..$ : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ... $ method :List of 4 ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ pca : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ ignore: chr(0) $ thresh : num 0.95 $ pcaComp : num 5 $ numComp : num 5 $ ica : NULL $ wildcards :List of 2 ..$ PCA: chr(0) ..$ ICA: chr(0) $ k : num 5 $ knnSummary :function (x, ...) $ bagImp : NULL $ median : NULL $ data : NULL - attr(*, "class")= chr "preProcess"
我们对三个插槽感兴趣。它们是 prePCA$mean, prePCA$std (常规化参数) 和 prePCA$rotation (旋转和负载矩阵)。
> str(env$preICA) List of 20 $ dim : int [1:2] 7906 11 $ bc : NULL $ yj : NULL $ et : NULL $ invHyperbolicSine: NULL $ mean : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ std : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ ranges : NULL $ rotation : NULL $ method :List of 4 ..$ ica : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ ignore: chr(0) $ thresh : num 0.95 $ pcaComp : NULL $ numComp : NULL $ ica :List of 3 ..$ row.norm: logi FALSE ..$ K : num [1:11, 1:3] -0.214 -0.0455 -0.2185 -0.0534 -0.1604 ... ..$ W : num [1:3, 1:3] -0.587 0.77 -0.25 -0.734 -0.636 ... $ wildcards :List of 2 ..$ PCA: chr(0) ..$ ICA: chr(0) $ k : num 5 $ knnSummary :function (x, ...) $ bagImp : NULL $ median : NULL $ data : NULL - attr(*, "class")= chr "preProcess"
此处我们有相同的 $mean 和 $std, 以及两个矩阵 $K 和 $W。计算 ICA 的 caret 软件包使用 fastICA 软件包和以下算法:
- 初始矩阵居中 (可能是行规范化), 我们得到 Х 矩阵
- 然后 Х 矩阵被投影到主分量的方向, 我们得到 PCA = X * K 作为结果
- 之后, PCA 乘以混合矩阵, 得到独立分量 ICA = X * K * W
我们按照两种方式使用 predict::caret 函数和 preProcess 函数获得的参数来计算 PCA 和 ICA。
require(magrittr)
evalq({
pca <- predict(prePCA, x.cap)
ica <- predict(preICA, x.cap)
pca1 <- ((x.cap %>% scale(prePCA$mean, prePCA$std)) %*%
prePCA$rotation)
ica1 <- ((x.cap %>% scale(preICA$mean, preICA$std)) %*%
preICA$ica$K) %*% preICA$ica$W
colnames(ica1) <- colnames(ica1, do.NULL = FALSE, prefix = 'ICA')
},env)
evalq(all_equal(pca, pca1), env)
# [1] TRUE
evalq(all_equal(ica, ica1), env)
# [1] TRUE
结果是相同的, 符合预期。
使用 pcaPP 软件包是计算 PCA 的更可靠方法。此方法更准确地标识主分量。
fastICA 软件包含有大量附加函数和参数, 可以更灵活, 更完整地计算独立分量。我建议使用 fastICA, 而不是 caret 中的函数。
2.3概率主分量分析 (PPCA)
PCA 有一个概率模型 – PPCA。以概率术语重新定义此方法具有许多优点。
- 有机会使用 ЕМ 算法来搜索解决方案。当 d ≪ D 的情形下, ЕМ 算法是一种更有效的计算过程
- 正确处理缺失值。它们被简单地添加到概率模型的隐藏变量列表中。然后将 ЕМ 算法应用于该模型。
- 有过渡到混合物分布模型的可能性, 拓宽了该方法的适用性
- 使用贝叶斯方法解决选择模型问题的可能性。特别地, 可以构建约化空间维度 d 的理论上合理的选择方案 (参见 [24,25])
- 从概率模型生成新对象的可能性
- 为了分类起见 – 单个对象类模型分布的可能性, 以便进一步在分类方案中使用
- likelihood 函数的值是一个通用准则, 允许不同的概率模型相互比较。具体来说, 可以使用 likelihood 值轻易地识别数据集合中的异常值。
与 PCA 的经典模型类似, 概率模型 PCA 与超平面中基础的选择在相关性上是不变的。
与 PCA 的经典模型不同, 只有超平面解释数据才能最好地恢复, 概率模型恢复了整个数据变异模型。顾名思义, 它描述了所有方向上的数据分散。所以, 该解决方案不仅包括由协方差矩阵的特征向量定义的超平面基本向量的方向, 而且还包括这些基本向量的长度。
若要使用 РРСА 和其它获得主分量的非线性方法, 可以使用 pcaMethods 软件包。
pcaMethods 软件包是一套 PCA 的各种实现, 以及用于交叉验证和结果可视化的工具。这些方法主要允许将 PCA 应用于不完整的数据集合, 因此可用于评估缺失值 (NA)。软件包可在储存库 Bioconductor 中找到, 可以按照下面的说明进行安装。
source("https://bioconductor.org/biocLite.R") biocLite("pcaMethods") library(pcaMethods)
软件包的所有方法返回包含结果的 pcaRes 通用类。这给了用户带来良好的灵活性。包装函数 pca() 可以通过其命名参数访问所有必需的 РСА 类型。以下是一个简要说明的算法列表:
- svdPCA 是标准函数 prcomp 的封装函数。
- svdImpute 是插补 NA 的算法实现。这对于大量 NA (>10%) 是宽容的。
- 概率 PCA (ppca)。PPCA 容忍的 NA 数量在 10% 至 15%之间。
- 贝叶斯 PCA (bpca)。类似于概率 PCA, 它使用 EM 方法与贝叶斯模型来计算恢复值的概率。此算法容忍相对较大数量的缺失数据 (>10%)。通过该方法获得的分值和负载与使用普通的 РСА 获得的分值和负载不同。事实上, BPCA 是 专为评估缺失值 而开发的, 且基于具有自动相关性识别 (ARD) 的变异贝叶斯框架 (VBF)。该算法不在负载之间强制正交性。事实上, BPCA 的作者发现包括正交准则令预测变得更糟。
- 逆向非线性 PCA (NLPCA) 最适合于预测因子与目标变量之间的关系是非线性的实验数据。NLPCA 基于关联神经网络 (autoencoder) 的解码部分的训练。可以在网络的隐藏层看到负载。在反向传播过程中, 误差计算忽略训练数据中的缺失值。这样, NLPCA 可以用于处理缺失值, 与标准的 РСА 相同。唯一的区别是现在由负载 P 代表神经网络。我们将在 “Autoencoder” 部分中更详细地研究这种降维方式。
- Nipals PCA 是通过迭代偏最小二乘法的非线性评估。这是 PLS 回归的一种核心算法, 它可以执行缺失值的 PCA, 将它们遗留在相应内部产品之外。它容忍少量 (通常不超过 5%) 的缺失数据。
- 局部最小二乘法 (LLS) 插补 是 llsImpute() 的算法/函数, 基于不完整变量的 k-最相邻线性组合评估缺失数据。变量之间的距离定义为 Pearson, Spearman 或 Kendall 相关系数的绝对值。最优线性组合可以通过求解局部最小二乘法问题找到。
在当前的实现中, 提出了两种评估缺失值的方法。这些方法略有不同。第一种方法是在全部的变量子集中搜索邻域限制。当未定义变量的数量相当低时, 首选此方法。第二种方法将所有变量视为候选。这里的缺失值首先由平均值替换。然后, 该方法使用当前评估作为 LLS 回归的输入进行迭代, 直到新旧评估的变化低于某一阈值 (0.001)
不幸地是, 本文的主题及其篇幅不允许我撰写有关这个辉煌软件包中所有建议的算法。与稍后的 autoencoder 相比, 我们只会查看 NLPCA。
2.4. Autoencoder
因为深度神经网络的出现, 自动关联网络已被广泛使用。在 我之前的一篇文章 中, 我们详细研究了训练 autoencoders (АЕ), 堆栈式 autoencoders, 受限玻尔兹曼机器 (RBM) 等的结构和特点。
Autoencoder 是具有一个或多个隐藏层的神经网络, 且输入层中的神经元数量等于输出层中神经元的数量。АЕ 的主要目的是尽可能准确地表示输入数据。用于标准神经网络训练的正则化和神经元激活方法也同样用于 AE。任何构建神经网络的软件包只要允许提取隐藏层权重矩阵, 均可用来构建 AE 模型, 。我们将使用 autoencoder 软件包。以下示例将有助于回顾可能的 AE 结构:
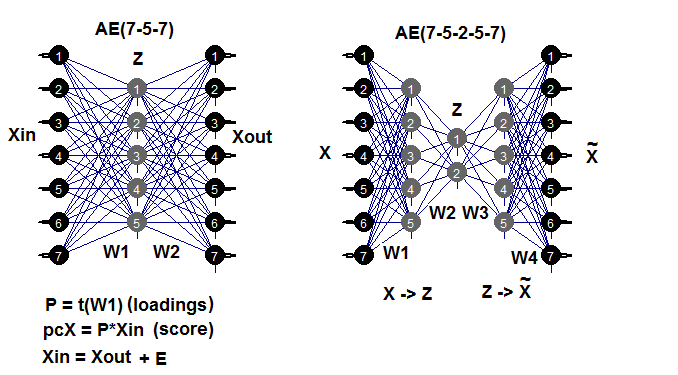
图例. 7. autoencoders 结构图 (三层和五层)
第一 (输入) 和隐藏层之间的权重矩阵 W1 是获得的负载作为训练结果。在将输入矩阵 Xin 投影 (乘法) 到负载 Р 上之后, 我们将获得一个约化矩阵 (基本上是主分量)。我们可以使用 predict() 得到相同的结果。此函数允许获取隐藏层的输出 (如果 hidden.output = TRUE), 或 autoencoder 的输出层 (如果 hidden.output = FALSE)。
训练 AE 后, 我们可以从模型中提取权重矩阵 W1 并恢复误差。如果我们也输入测试数据集合, 那么我们也可以从模型中获取测试误差。训练误差在很大程度上取决于 AE 的参数, 甚至取决于 n.hidden/n.in 的比例。这个比例越大, 复原的误差越大。如果我们旨在实现显著的降维, 则可以连续连接两个 AE。例如, 如果有 12 个输入, 我们可以训练一个模型 12-7-12, 从隐藏层执行 predict() 并将其输入到 autoencoder 7-3-7。减少的数字将为 12 -> 3。实验快乐!
应当提到的是, 尽管软件包宣称具有创建和训练多层 AE 的能力, 但我无法做到这一点。
我们来进行一些实验。您已经有了本文第一部分的 Part_1.RData 计算结果。以下是计算顺序:
- 从 dataSet 集合中创建训练/验证/测试数据集合, 并获取 DT 列表;
- 插补异常值并获取 DTcap 列表;
- 使用带 (“center”, “scale”, “spatialSign”) 的方法将我们的集合进行常规化。您可以使用我们以前研究的其它变换和常规化方法;
- 在隐藏层中用三个神经元训练 autoencoder 模型。您可以探索其它变种。随着神经元数量的增加, 恢复误差降低;
- 使用已训练模型和 predict(), 从隐藏层获得结果。这基本上是一个约化矩阵 (РСА)。向其添加目标变量;
- 绘制变体和训练/验证测试约化样本协方差的图表。
require(FCNN4R)
require(deepnet)
require(darch)
require(tidyverse)
require(magrittr)
#----清理---------------------
require(caret)
require(pipeR)
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
dataSet %>%
preProcess(., method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
rm(dataSetClean, train, val, test)
},
env)
#------异常值-------------
require(foreach)
evalq({
DTcap <- list()
foreach(i = 1:3) %do% {
DT[[i]] %>%
select(-c(Data, Class)) %>%
as.data.frame() -> x
if (i == 1) {
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> DTcap
foreach(i = 1:3) %do% {
cbind(DTcap[[i]], Class = DT[[i]]$Class)
} -> DTcap
DTcap$train <- DTcap[[1]]
DTcap$val <- DTcap[[2]]
DTcap$test <- DTcap[[3]]
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
#------常规化-----------
evalq(
{
method <- c("center", "scale", "spatialSign") #, "expoTrans") #"YeoJohnson",
# "spatialSign"
preProcess(DTcap$train, method = method) -> preproc
list(train = predict(preproc, DTcap$train),
val = predict(preproc, DTcap$val),
test = predict(preproc, DTcap$test)
) -> DTcap.n
#foreach(i = 1:3) %do% {
# cbind(DTcap.n[[i]], Class = DT[[i]]$Class)
#} -> DTcap.n
},
env)
#----训练-------
require(autoencoder)
evalq({
train <- DTcap.n$train %>% select(-Class) %>% as.matrix()
val <- DTcap.n$val %>% select(-Class) %>% as.matrix()
test <- DTcap.n$test %>% select(-Class) %>% as.matrix()
## 设置 autoencoder 架构:
nl = 3 ## number of layers (default is 3: input, hidden, output)
unit.type = "tanh" ## specify the network unit type, i.e., the unit's
## 激活函数 ("logistic" 或 "tanh")
N.input = ncol(train) ## 输 层中的单位数 (每像素一个单位)
N.hidden = 3 ## 隐藏层中的单位数
lambda = 0.0002 ## 重量衰减参数
beta = 0 ## 稀疏项权重系数
rho = 0.01 ## 期望的稀疏参数
epsilon <- 0.001 ## 用于初始化权重的小参数
## 来自 N(0,epsilon^2) 的样本作为小高斯随机数
max.iterations = 3000 ## 优化器中的迭代次数
## 使用 BFGS 训练 autoencoder
## 优化方法
AE_13 <- autoencode(X.train = train, X.test = val,
nl = nl, N.hidden = N.hidden,
unit.type = unit.type,
lambda = lambda,
beta = beta,
rho = rho,
epsilon = epsilon,
optim.method = "BFGS", #"BFGS", "L-BFGS-B", "CG"
max.iterations = max.iterations,
rescale.flag = FALSE,
rescaling.offset = 0.001)}, env)
## 训练和测试集合的平均方差报告:
#cat("autoencode(): mean squared error for training set: ",
# round(env$AE_13$mean.error.training.set,3),"/n")
## 从 autoencoder.object 提取权重 W 和偏差 b:
#evalq(P <- AE_13$W, env)
#-----predict-----------
evalq({
#Train <- predict(AE_13, X.input = train, hidden.output = FALSE)
pcTrain <- predict(AE_13, X.input = train, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$train$Class)
#Val <- predict(AE_13, X.input = val, hidden.output = FALSE)
pcVal <- predict(AE_13, X.input = val, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$val$Class)
#Test <- predict(AE_13, X.input = test, hidden.output = FALSE)
pcTest <- predict(AE_13, X.input = test, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$test$Class)
}, env)
#-----图形---------------
require(GGally)
evalq({
ggpairs(pcTrain,columns = 1:ncol(pcTrain),
mapping = aes(color = Class),
title = "pcTrain")},
env)
evalq({
ggpairs(pcVal,columns = 1:ncol(pcVal),
mapping = aes(color = Class),
title = "pcVal")},
env)
evalq({
ggpairs(pcTest,columns = 1:ncol(pcTest),
mapping = aes(color = Class),
title = "pcTest")},
env)
我们来查看图表
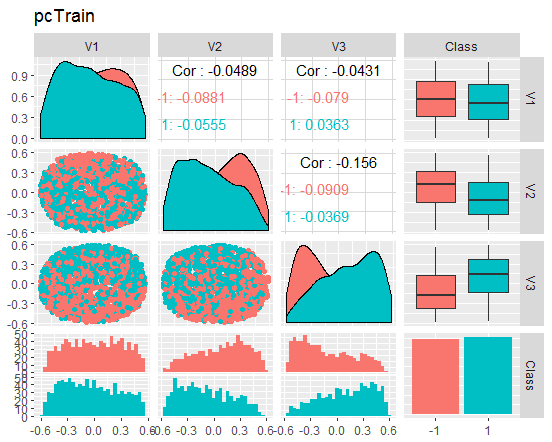
图例. 8. 约化训练集合的变体和协方差
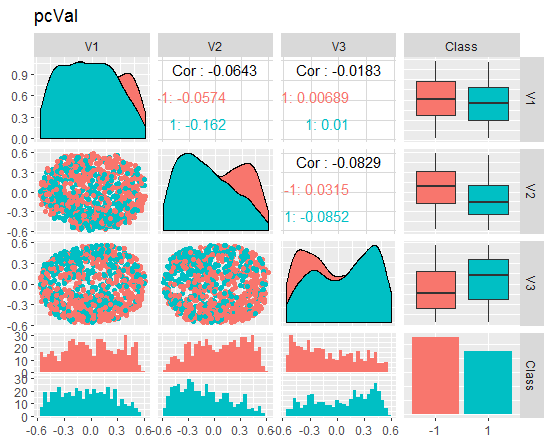
图例. 9. 约化验证集合的变体和协方差
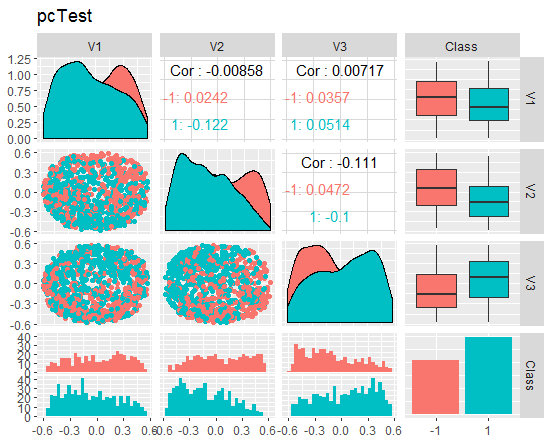
图例. 10. 约化测试集合的变体和协方差
这些图表能告诉我们什么? 我们能够看出, 主分量部分 (V1, V2, V3) 是由目标变量等级分割。训练/验证/试验集合的分布是偏斜的。我们应去除噪音样本, 看看是否能改善图像。您可以自行完成。
小的题外话: NLPCA
为了能够通过主分量切分数据, 重要的是区分 纯降维 的应用和主要关注标识以及唯一性和有意义的分量识别 (通常称为 特征提取) 的应用程序。
具有降噪和压缩数据的纯降维应用只需要具有高描述能力的子空间。单独分量令此子空间的方式不受限制, 因此不必是唯一的。唯一的要求是子空间提供关于均方误差 (MSE) 的最大信息。作为覆盖该子空间的单独分量, 由算法进行处理, 无任何设定顺序或微分称量, 这被称为 对称训练类型。这种类型的训练包括由标准自动关联神经网络 (autoencoder) 执行的非线性 PCA, 因此被称为 s-NLPCA。在文章的前一部分我们已研究过这个变体。
非线性分层 PCA (h-NLPCA) 不仅提供了由分量覆盖的最优非线性子空间, 而且还通过与标准 PCA 中的线性分量相似的等级顺序来限制非线性分量。在上下文中的层次结构由两个重要的属性来解释 – 可伸缩性和稳定性。可伸缩性意味着前 n 个分量解释可以被 n 维子空间覆盖的最大色散。稳定性意味着 n-分量的第 i 个分量与 m-分量的第 i 个分量相同。
分层顺序产生不相关的分量。非线性也意味着 h-NLPCA 能够去除分量之间的复杂非线性相关性。这有助于过滤有用和有意义的分量。此外, 将非线性不相关分量缩放为单位色散, 我们获得复杂的非线性白化 (球形变换)。对于像是回归、分类或源头盲分的应用程序的初步处理很有用处。由于非线性白化 消除数据中的非线性关系, 进一步使用的方法可以是线性的。这对于 ICA 尤其重要, 可以通过使用这种非线性白化来扩展到非线性方法。
我们如何达成分层顺序?通过色散将对称处理的分量简单排序不会产生所需的分层顺序 – 既不是线性的, 也不是非线性的。可以通过两种相互关联的方法来实现层次结构: 通过限制分量空间中的色散, 或限制原始空间中重建的平方差。类似于线性 PCA, 第 i 个分量必须要考虑到最高的第 i 个色散。
在非线性情况下, 这种限制可能是无效的或非单调的, 无需额外的限制。与之对比, 复原误差可以被控制得更好, 因为对于变换中的任意缩放它的绝对值不变。因此, 误差的层级限制是更有效的方法。在简单的线性情况下, 我们可以通过 顺序方法 实现分量的分层排列, 从前一色散的平方差所定义的剩余色散中逐一提取分量。在非线性的情况下, 并行训练若干网络期间, 这即非顺序也非同时工作。剩余色散不能用平方差来解释, 且与非线性变换无关。解决方案是仅使用一个具有子网层次结构的神经网络。这可令我们在误差函数中立即制定层次结构。
2.5. 逆向非线性 PCA
在本文的这一部分当中, 非线性 PCA 将解决一个逆向问题。而原来的问题是预测来自设定输入的输出, 逆向问题是对最佳匹配集合结果的输入进行评估。由于我们既不知道模型, 也不知道数据生成的过程, 我们要体现一个所谓的盲眼逆转问题。
取决于是否将所需的分量作为输出预测, 或通过相应的算法评估为输入数据, 简单的线性 PCA 可以同时考虑原始和逆向问题。自动关联网络 (АЕ) 同时对直接和逆向模型建模。
直接模型由 АЕ 第一部分通过提取函数 Fextr: X→Z 来定义。逆向模型由 AE 第二部分通过生成函数 Fgen: Z→X 来定义。第一个模型更适合于线性 PCA, 且在非线性 PCA 的情况下不起作用。发生这种情况是因为这种模式可能非常复杂, 因为 “一对多” 的问题难以解决。两个相同的集合 X 可以对应于 Z 分量的不同值。
逆向非线性 PCA 仅需要自动关联网络的第二部分 (图例.11), 由网络 3-7-12 描绘。此世代的这一部分是 Fgen 的逆向反射, Fgen 从它们的低维图像 Z 生成或重建 Х 的大尺寸形态。分量 Z 的这些值现在是未知输入, 其可以将传播的部分误差 σ 返回到输入层 Z。
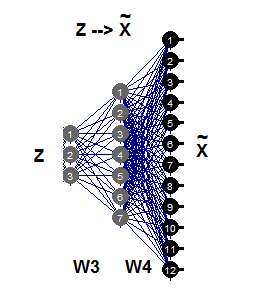
图例. 11. 逆向非线性 PCA
我们来比较使用 AE 与使用 nlpca::pcaMethods 函数获得的结果。此函数在本文前面提到过。针对相同的数据按照相同的初始约化需求 12-> 3 进行计算并进行比较。
为此, 请使用 DTcap.n$train 集合, 删除目标变量 Class 并将其转换为矩阵。集合中心化。神经网络的结构设置为 (3,8,12), 其余参数可以在下面的脚本中找到。获得结果之后, 单取主分量 (分值), 将目标变量添加到其中并绘制图表。
应当提到的是, 这个算法非常慢, 每次全新启动过程都会产生与前一个不同的新结果。
require(pcaMethods)
evalq({
DTcap.n$train %>% tbl_df %>%
select(-Class) %>% as.matrix() %>%
prep(scale = "none", center = TRUE) -> train
resNLPCA <- pca(train,
method = "nlpca", weightDecay = 0.01,
unitsPerLayer = c(3, 8, 12),
center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
nPcs = 3, completeObs = FALSE,
subset = NULL, cv = "none", # "none""q2"), ...)
maxSteps = 1100)
rm(train)},
env)
#--------
evalq(
pcTrain <- resNLPCA@scores %>% tbl_df %>%
cbind(., Class = DTcap.n$train$Class)
, env)
#------graph-------
require(GGally)
evalq({
ggpairs(pcTrain,columns = 1:ncol(pcTrain),
mapping = aes(color = Class),
title = "pcTrain -> NLPCA(3-8-12) wd = 0.01")},
env)
#----------
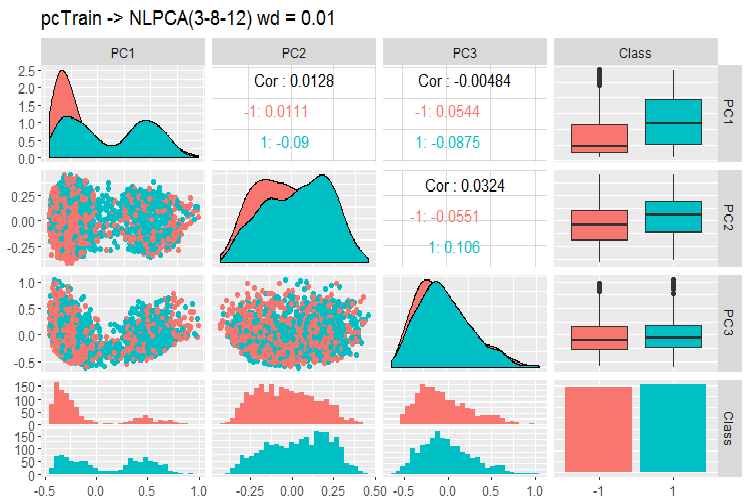
图例. 12. 使用 NLPCA 的主分量变体和协方差
我们在这张图表上可以看到什么?主分量由目标变量的等级分割, 并具有非常低的相关性。第三个分量看起来没必要。我们来查看模型的一般信息。
> print(env$resNLPCA) nlpca calculated PCA Importance of component(s): PC1 PC2 PC3 R2 0.3769 0.2718 0.09731 Cumulative R2 0.3769 0.6487 0.74599 12 Variables 2000 Samples 0 NAs ( 0 %) 3 Calculated component(s) Data was mean centered before running PCA Data was NOT scaled before running PCA Scores structure: [1] 2000 3 Loadings structure: Inverse hierarchical neural network architecture 3 8 12 Functions in layers linr tanh linr hierarchic layer: 1 hierarchic coefficients: 1 1 1 0.01 scaling factor: 0.3260982
这里有一个问题。结果不返回权重矩阵 W3 和 W4。换言之, 我们没有负载 P, 我们不能在测试和验证集合上获得主分量 S (分值)。这个问题在降维的两个其它方法中也存在 – tSNE, ICS。我们可以很容易地合理解决这些问题, 但我们最好不要走一条未知结果的路线。
软件包含有另两种方法 – 概率和贝叶斯 PCA。它们快速和并回的负载, 这允许轻易地获得验证和测试集合上的主分量。我仅带来了一个 PPCA 的例子。
#=======PPCA===================
evalq({
DTcap.n$train %>% tbl_df %>%
select(-Class) %>% as.matrix() -> train
DTcap.n$val %>% tbl_df %>%
select(-Class) %>% as.matrix() -> val
DTcap.n$test %>% tbl_df %>%
select(-Class) %>% as.matrix() -> test
resPPCA <- pca(train, method = "ppca",
center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
nPcs = 3, completeObs = FALSE,
subset = NULL, cv = "none", # "none""q2"), ...)
maxIterations = 3000)
},
env)
#-----------
>print(env$resPPCA)
ppca calculated PCA
Importance of component(s):
PC1 PC2 PC3
R2 0.2873 0.2499 0.1881
Cumulative R2 0.2873 0.5372 0.7253
12 Variables
2000 Samples
0 NAs ( 0 %)
3 Calculated component(s)
Data was mean centered before running PCA
Data was NOT scaled before running PCA
Scores structure:
[1] 2000 3
Loadings structure:
[1] 12 3
为分量 1 和 2 绘制负载和分值图表:
slplot(env$resPPCA, pcs = c(1,2), lcex = 0.9, sub = "Probabilistic PCA")
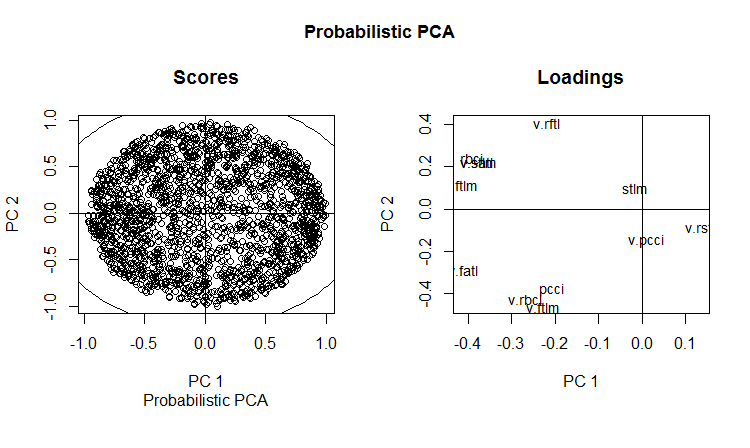
图例. 13. 概率 PCA 的 РС1 和 РС2 (负载和分值)
PPCA 训练/验证/测试集合的主分量的变体和协方差图表如下所示。您可在 GitHub 上找到脚本。
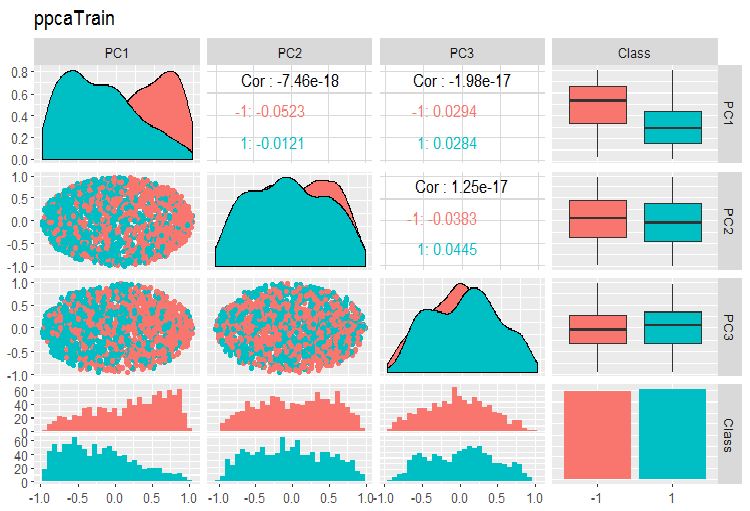
图例. 14. 利用 PPCA 获得的训练集合的主分量的变体和协方差
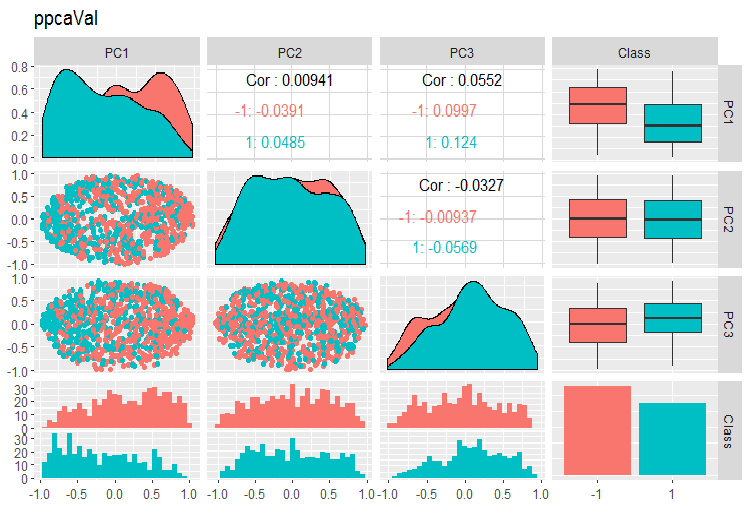
图例. 15. 利用 PPCA 获得的验证集合的主分量的变体和协方差
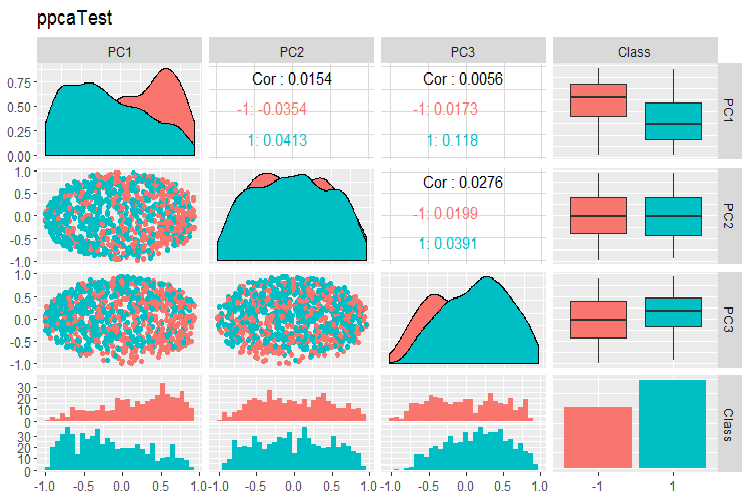
图例. 16. 利用 PPCA 获得的测试集合的主分量的变体和协方差
由目标变量的等级分割获得的 PPCA 主分量, 与使用先前研究的 autoencoder 的同等约化相比, 未能取得更佳品质。PPCA 和 BPCA 的优点是速度和简单性。品质应该使用某种分类模型进行评估。
3. 将数据集合划分为训练/验证/测试集合
在这部分中, 一切都保持与前面文章中描述的一样。训练期间: 训练/验证/测试, 滑动窗口, 成长窗口, 间或引导。在选择模型时: 交叉验证。识别这些集合有足够的大小仍然是一个悬而未决的问题。
我想提一下 Win Wector 有限公司 的有趣声明, 关于在预处理变换期间使用训练集合, 他们说, 如果在训练集合上确定了主分量, 则模型应使用在验证数据集合上获得的主分量进行训练。这意味着使用的集合不能用于训练模型。这可以在网络训练时进行测试。
结束语
我们已经研究了为训练深度神经网络而进行的数据准备的几乎所有阶段。如您所见, 这是一个复杂而耗时的阶段, 需要良好的理论知识。未能理解和掌握每个阶段的数据准备技能, 所有进一步的行动都没有意义。
在数据准备的阶段, 所有计算若无直观控制, 就不可能取得良好效果。不耐烦和懒惰者可享受 “preprocomb” 和 “metaheur” 软件包, 它们有助于自动寻找初步准备的最适合阶段。
应用
本文中使用的脚本可在 GitHub/Part_III 上找到。
本文译自 MetaQuotes Software Corp. 撰写的俄文原文
原文地址: https://www.mql5.com/ru/articles/3526
MyFxtop迈投-靠谱的外汇跟单社区,免费跟随高手做交易!
免责声明:本文系转载自网络,如有侵犯,请联系我们立即删除,另:本文仅代表作者个人观点,与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。

 MyFxTops邁投財經
MyFxTops邁投財經
