介绍

许多人认为根本分析很难理解。目前还不清楚如何掌握关键点以及需要选择哪些参数。很难找到影响重大的参数及其时间跨度。

2011年，我偶然发现了文章多元还原分析。策略生成器和测试人员结合在一起，发现其中描述的方法很有趣。本文研究了这种基本分析方法的应用，并对其结果进行了描述。

什么是多变量约简分析？

多元归约分析是一种从两个或多个自变量估计一个因变量相关性的方法。

非数学思维可能无法理解这个定义。以下示例将说明此分析的含义以及如何使用它。

想象一下，一个研究人员在服用补充剂时，试图估计正常的身体活动的效率。研究人员对24所大学的学生进行了实验。学生们分成四组，每组六人。第一组每天补充100毫克，第二组每天补充200毫克，第三组每天补充300毫克，第四组每天补充400毫克。这项实验包括四个层次的补充摄入量和三个层次的体育活动。每组6人分成3对。第一组每周运动0小时，第二组每周运动5小时，第三组每周运动10小时。实验结束后，每个参与者都减肥了。数据已输入下表：

实验参与者	补充剂量（mg/d）	体力活动水平（小时/周）	体重减轻（磅）
一	一百	零	– 4
二	一百	零	零
三	一百	五	– 7
四	一百	五	– 6
五	一百	十	– 2
六	一百	十	– 14
七	二百	零	– 5
八	二百	零	– 2
九	二百	五	– 5
十	二百	五	– 8
十一	二百	十	– 9
十二	二百	十	– 9
十三	三百	零	一
十四	三百	零	零
十五	三百	五	– 3
十六	三百	五	– 3
十七	三百	十	– 8
十八	三百	十	– 12
十九	四百	零	– 5
二十	四百	零	– 4
二十一	四百	五	– 4
二十二	四百	五	– 6
二十三	四百	十	– 9
二十四	四百	十	– 7

每位参与者的减肥结果

所以我们有两个问题：

1. 是什么导致了这种减肥——补充剂还是体力活动？
2. 体重变化与影响因素有什么关系？

这和金融市场上常见的情况非常相似，不是吗？例如，当一种货币的价格发生变化时，人们总是问它受到什么新闻的影响。如果有经济因素影响价格，那么当这个因素向多个方向变化时，价格应该如何变化？

多元回归分析和程序统计有助于回答这些问题。传入或导入包含数据的表，然后从菜单中选择“多重回归”：

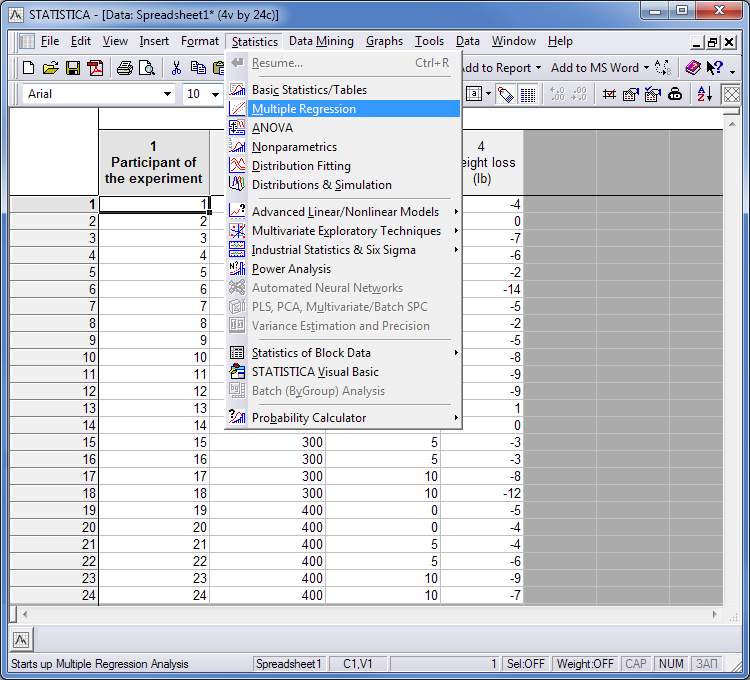
传说。1。将样本数据导入统计

选择菜单项后，找到“变量”按钮并单击它：

传说。2。多元分析参数屏

它弹出一个窗口，选择变量进行分析。它由两部分组成：我们能在左手选择什么，我们相信什么是因变量（在我们的例子中，它减轻了重量），在右手，我们能选择什么来影响这些变化。

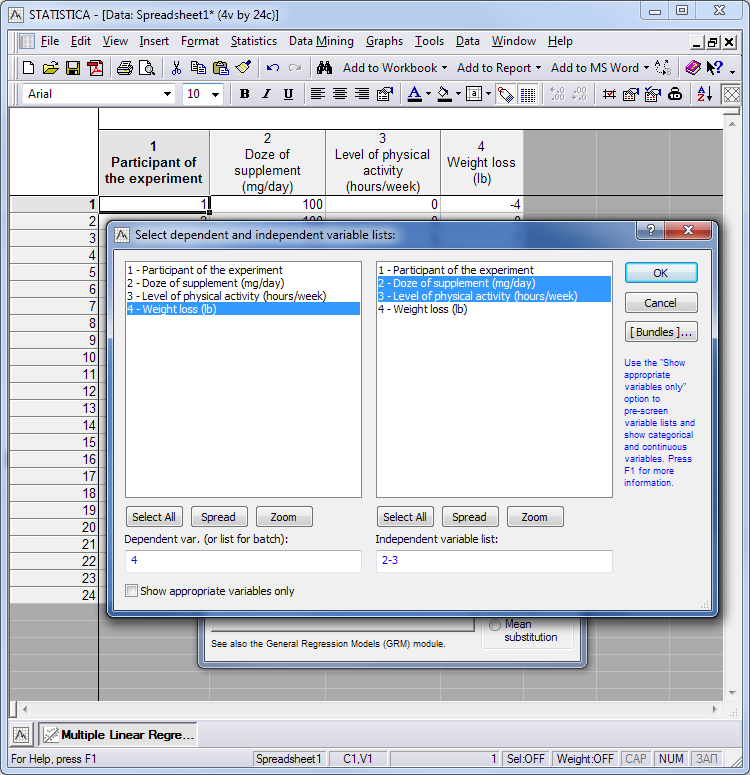
传说。三。因变量和自变量的分布

按“确定”返回到上一个设置对话框窗口。我们必须选中一个复选框，然后按“确定”：

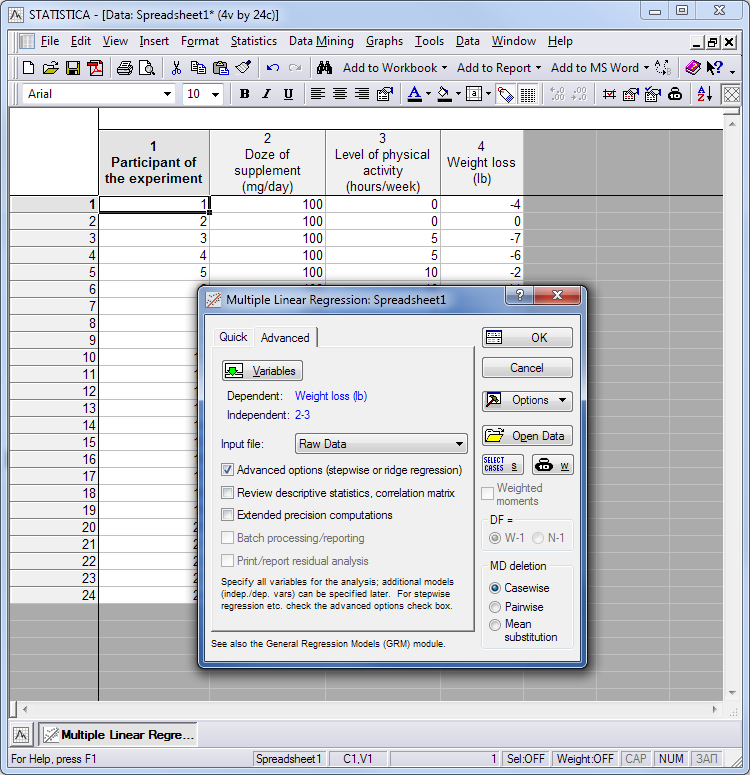
传说。4。多元分析参数的选择

在下面的窗口中，我们选择“所有效果”方法：

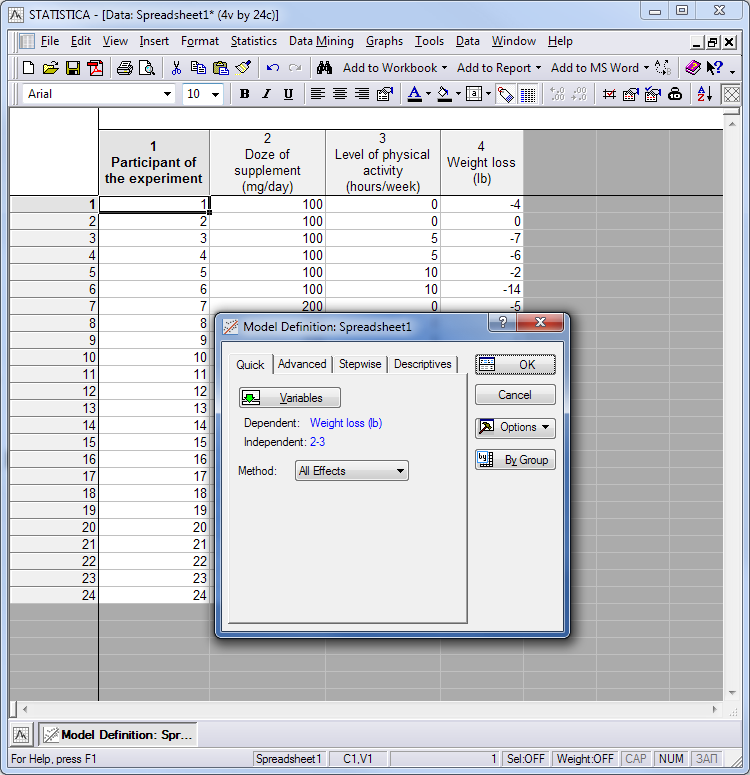
传说。5。选择方法

在所有的操作之后，我们将得到分析结果的窗口。统计数据显示，影响结果的因素以红色字体显示在列表中（在我们的示例中，“体力活动水平”）。其他变量：

• ‘案例数量’是事件分析的数量；
• “p”是相关的统计有效性水平（低于0.05的水平被认为是可靠的）；
• multiple r是方程因变量和自变量之间的多元相关值。

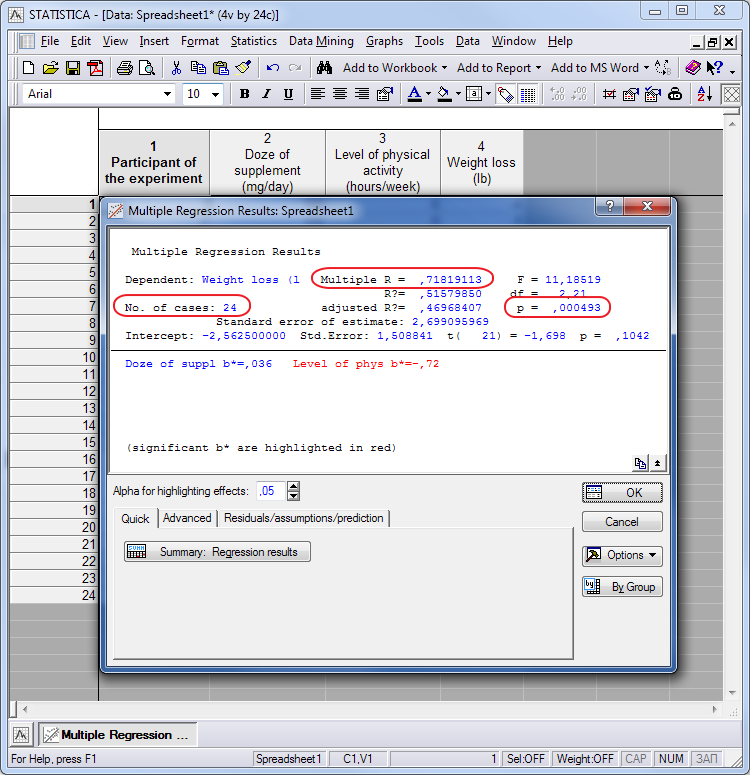
图形图例。6。数据处理结果

值“multiple r=071819113”可以解释为“multiple r”。失重与影响因素的多元相关系数为71.82%。

两个因素之一，“身体活动水平”是红色文字。这个因素是补充不足对减肥的影响。

现在我们只需要使用一个暂定的减量方程来计算这个因素是如何影响体重减轻的。要执行此操作，请按“摘要：回归结果”按钮弹出一个新表单。通过使用表中垂直列“b”的值来完成简化方程：

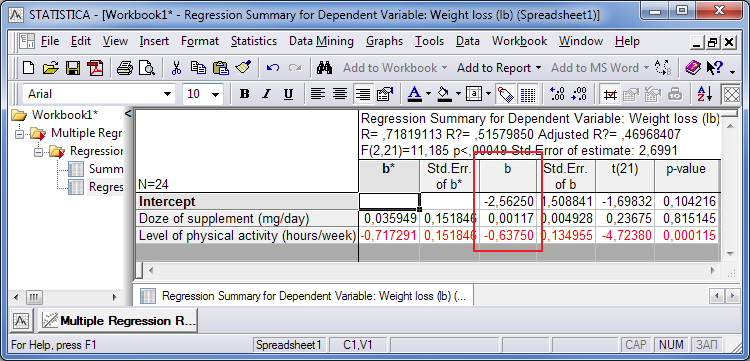
图形图例。7。约化方程的变量

我们得到如下方程：

通过替换方程式中的值（从统计中的ctrl+c-&gt到excel中的ctrl+v），我们可以计算补充摄入量和体力活动强度对体重变化的影响。例如：

• 重量变化1=0.00117*100-0.6375*0-2.5625=24455。这意味着，一个人每天服用100毫克，而不进行任何锻炼，可以减轻2.4磅的体重。
• 重量变化2=0.00117*100-0.6375*10-2.5625=88205。这意味着每天服用100毫克的补充剂，每周运动10小时，可使体重减轻8.82磅。

我希望这个例子澄清了多元分析的作用。事实上，有些人可能会发现它对自我检查很有用，比如他们的饮食是否有效，是否需要去健身房。

现在，我们要把我们从实验中学到的想法应用到钱上。假设欧元兑美元汇率对的价格变化是因变量，流行资源外汇工厂事件日历中的宏观经济统计数据是独立变量。

与上述例子类似，我们可以通过多元分析找出影响货币价格的宏观因素。我们还可以列出一个等式，当宏观经济统计数据公布时，估计货币价格的价值。

准备数据并将其导入程序统计。

当我与外汇工厂的网站合作时，我遇到了以下问题，我强烈建议考虑。在这个资源中，相同的数据以不同的格式发布。例如，数字可以是文本格式或附加文本数据，这使得正常收集数据变得困难。分析网站以收集数据可能会失败。

在过去的几年中，我从新闻日历中手动收集了美国的所有99个因子值。

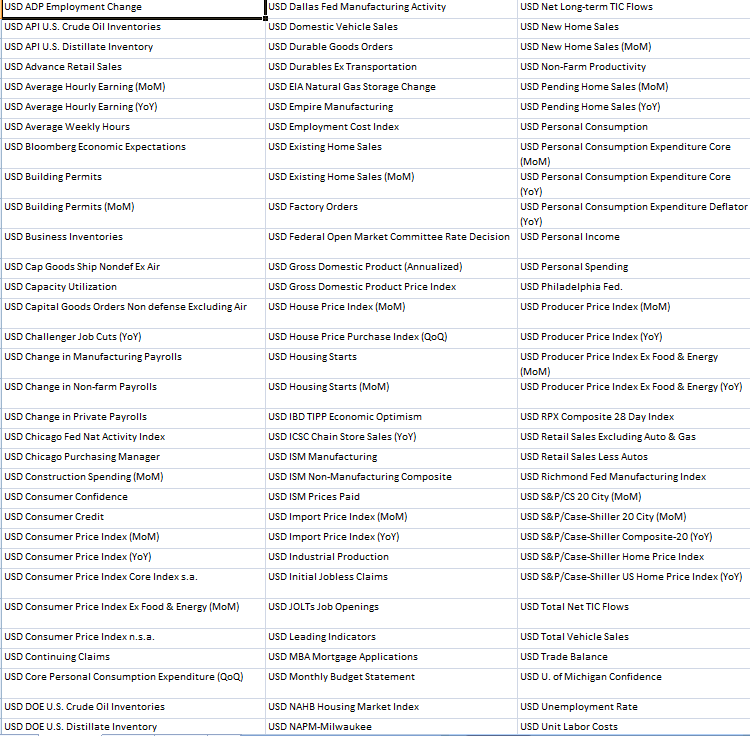
图8。公布的美国宏观经济指数

我以统一格式处理了所有数字，删除了诸如“百万”和“十亿”等附加文本，并将所有数据分为七列（参见本文附件中的“calendarusd.zip”文件），以及增加了欧元兑美元汇率1周期的报价。

列标题：

• 日期
• 月年
• 时间
• 时区
• 货币
• 描述
• 前置值

结果表包含6700多个宏观经济数据和欧元兑美元的报价，对简单的人工分析没有实际意义。在单独的列中按类型排序并按日期行之后，将所有数据导入表需要额外的处理器。我们使用脚本listconverttotable来处理数据并将其转换为表。

在“脚本设置”对话框窗口中，需要命名输入文件和目标文件。输入文件必须放在终端数据目录/mql5/files中，将在其中创建输出文件。

由于数据量大，消息列表的处理可能需要相当长的时间。警报内置在脚本中，它将指示处于哪个阶段。警报’8’会让你知道过程的结束，你可以使用文件。多元分析处理的表格将附在本文件之后。

我得到了以下结果（见附件“calendar-usd-out.zip”）：

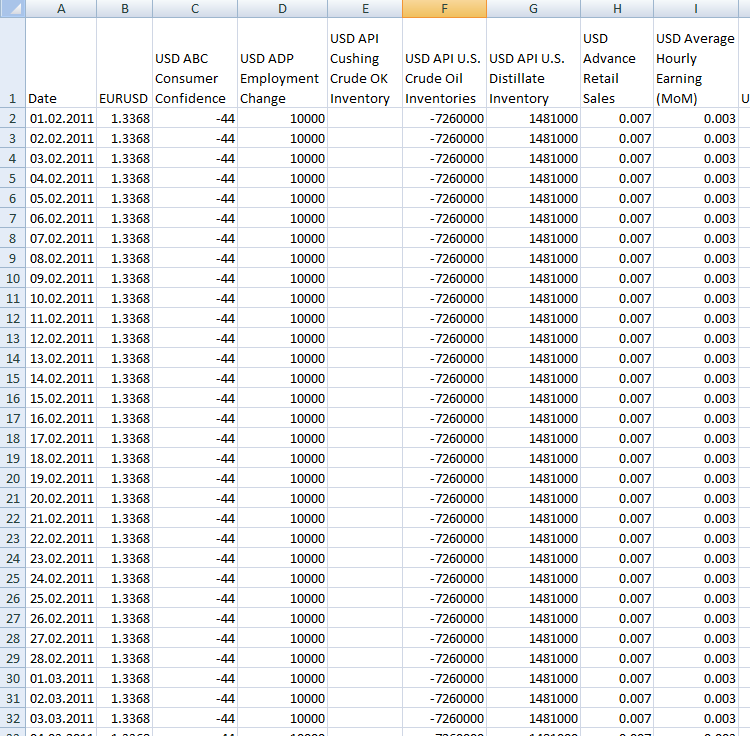
传说。9。ListConvertToTable脚本执行结果

我们将再次使用statistica来处理数据。要将csv文件上载到statistica，请执行以下步骤：

• 在statistica中打开“file”，然后选择“open”，选择排序类型“data files”，然后打开csv文件。
• 在窗口中，文本文件导入类型保留为“分隔”并按“确定”。
• 在打开的窗口中包含带下划线的项目
• “十进制分隔符”字段中必须有一个句点，无论是否为：

0

传说。10。在中导入表。csv格式到程序统计

按“确定”，您将得到一个包含您的数据的表。多元回归分析的数据准备就绪。为了分析数据对以下价格变动的影响，有必要增加价格变动周期。我从2010年开始选择消息，并有三个选项来分析因变量。

• 货币价格在新闻发布后一天发生变化；
• 货币价格在新闻发布五天后发生变化；
• 货币价格在新闻发布后10天发生变化。

这些列可以在导出到程序统计表或程序窗口之前手动添加到csv文件中：

1

传说。11。扩展数据表

数据已经准备好了，从中我们可以看到影响汇率的原因。

诱发因素对货币价格有很大的影响。

启动还原分析（“统计”-&gt；“多重回归”）。在拆分窗口的卡“高级”中启用标记项。按下“变量”按钮。

在第一个字段中，选择因变量，在第二个字段中，选择自变量。我们的公式将基于所选变量的值：

2

传说。12。用于选择指示器的窗口

使用按钮“变量”，选择要分析的数据：

3

传说。13。因变量和自变量的分布

将出现一个带有“某些变量没有方差”的警告窗口，指示某些选定变量不能留空。必须删除这些列。排除后，我们找到第49列“美元联邦公开市场委员会利率决定”，将其删除，并得到分析表（见附件“calendar_2010-2011_usd_out.zip”）。

单击确定。在打开的窗口中，我们选中“高级”选项卡中的相应复选框：

4

传说。14。选择方法逐步前进

按“确定”按钮完成选项选择。在下一个窗口中，选择“前进逐步”方法以启用自动数据选择，然后再次按“确定”：

5

传说。15。选择方法逐步前进

我们都处在冲刺阶段。当您在新窗口中看到成功的恢复分析消息时，请按按钮“摘要：回归结果”。

自动选择指标，选择那些对自变量和因变量之间的多元相关性贡献最大的指标。在我们的例子中，这是一组对价格影响最大的指标。从本质上讲，自动选择扮演着战略发生器的角色。生成的方程将只包括那些描述最可靠的价格行为方法的指标。

我必须指出，用于统计分析的指标包含规则，并不总是优化的。例如，简化方程可能包含大量不可靠的指标（结果表中的黑色字体）。如果列表中包含不可靠的指标，请返回到选择指标的阶段，并从大量指标中删除不可靠的指标进行分析。

返回分析结果窗口中的“取消”，然后重复分析。以这种方式排除所有不可靠的指标。同时，应记住，获得的多元相关值（多重r）不应明显小于初始值。您可以逐个从分析中删除所有不可靠的指标，或者将它们放在一起。首选第一种方法。

最后，只有影响价格波动的可靠指标仍在表中。在该表中，影响价格的变量以红色和黑色突出显示，零效果。

分析完成后，发现一些指标在公布后会对货币价格产生影响。每个周期的指标集是不同的。在窗口的左侧，选择“1天内价格变化”（即在指数发布后一天分析价格行为）作为一个独立变量，我们将得到以下结果：

6

传说。16。独立变量‘1天价格变化’

单击“取消”返回并选择“变量”返回变量选择窗体。逐渐地，我们从变量列表中删除黑色条目，只留下红色条目。其余条目中包含的信息将影响第二天的价格。

请注意，表中的条目有不同的颜色。自变量对因变量有显著影响，使用红色。下图中，所有条目都是红色的，即输入数据后，方程的误差结果小于第一种情况下的误差结果。影响程度可以通过最后一列中的“p值”系数来评估（值越小越好）。根据这些系数，可以去除价格影响为零的变量。

选择“5天内价格变化”，逐步删除无关项目，整理出有意义的新闻。我们将得到以下结果：

7

传说。17。独立变量‘5天内价格变化’

最后，我们选择“10天内价格变化”作为自变量，我们将得到：

8

传说。18。独立变量‘5天内价格变化’

当我们选择一个独立变量时，我们可以看到，从2010年到2011年中期，价格主要受到里士满研究所发布的房地产开发和指数的影响。

数据发布后5天，将生产和非生产行业指数、劳动力成本和失业指数添加到发展行业数据中。

当我们考虑10天的时候，影响指数会跳起来。生产和非生产性行业指数、住房开发与应用、失业率和能源价格都走在了前列。

因此，影响欧元兑美元汇率的因素与宏观基础数据分析非常相似，在所有教材中都会强调这些因素的重要性。如我们所见，它是由数学和统计学证明的。

约化方程与结果预测

仅仅知道影响价格的因素是不够的。重要的是能够估计数据发布后价格的变化。为此，我们将列出一个约化方程，正如本文开头所做的那样。

我们将根据图例中的“5天内价格变化”表建立数值列折减方程。17。为此，我们将使用标题为“b”的列中的变量。第一行是数字常数，在分析结束时得到。其计算如下。

让我们根据这些系数来建立约化方程：

在这里，我们使用“b”列中的值作为系数，使用已发布的宏观经济数据作为方括号中的乘数。

将源网站上公布的宏观经济指数的值输入方程，得到一个R值，大于或小于0。如果输入新数据的结果大于零，则表示该期间价格上涨，并选择进行分析。R值表示价格增长。负r表示价格更低。在这种情况下，R值表示价格下降。

将数值代入上述公式，并以欧元兑美元为例对计算结果进行了考虑。我们将以2010年8月4日的输入数据为例，将系数代入方程：

	乙	价值	[B] [值]
拦截	-0.0761	一	-0.0761
1天内价格变化	零点三五五一	-0.00	-0.00
10天内价格变化	零点三一九九	零点零二四四	零点零零七八
美元现房销售（MOM）	零点四五五二	-0.022	-0.0100
美元MBA抵押贷款申请	-0.1470	-0.044	零点零零六五
美元就业成本指数	一百四十四点零零四一	零点零零六	零点八六四零
百万美元密尔沃基	零点零一零六	五十九	零点六二七八
美元现房销售	零	伍佰陆拾陆万元	-0.65 96
美元失业率	-67866	零点零九九	-0.67
美元ISM制造	零点零一九七	五十六点二	一点零五二
美元资本货物订单非防务，不包括空运	-2.8934	零点零四八	-0.1389%
美元耐用品，不含运费	四点九二九零	零点零一二	零点零五九一
美元房价购买指数（QoQ）	-5.929	-0.018	零点一零六七
美元芝加哥采购经理	-0.0160	五十九点一	-0.9433
美元个人消费支出核心（同比）	-19.857	零点零一五	-0.29 79
			-0.0230

R=-00230，所以接下来的五天继续下跌，从2010年4月8日起，价格下跌了-230点。让我们看看这段时间内欧元兑美元的货币对图表：

9

传说。19。欧元兑美元8.2010

从图表中可以看出，预测是准确的。在五个交易日，价格从1.3154下跌至1.2844（8月11日收盘），或-310。证明了基于约化方程结果预测的价格下跌。同样，其他日期也可以替换。

结论

本文所研究的宏观经济数据分析可以简化和自动分析基本面，因此即使是新手也可以处理大量的经济数据。

此外，这种基本方法提供了一个机会，可以立即对信息作出反应，并调整交易。

请注意，预测不能被视为货币价格将朝着预期方向变化的绝对保证。预测结果只是概率，取决于许多因素。此外，当新数据到达时，将重新计算简化方程。

祝你好运！