MyFxTops邁投財經简介
本文“指数平滑法时间序列预测”[1]简要总结了指数平滑模型，并举例说明了优化模型参数的可能方案。最后，提出了基于线性衰减增长模型的预测指标。本文试图在一定程度上提高预测指标的准确性。
货币报价的预测，即使提前三、四步，也是非常可靠和复杂的。然而，在本系列的前一篇文章中，我们预测了前面12个步骤，并清楚地认识到，在这么长的时间内，无法取得令人满意的结果。因此，对于置信区间最窄的预测的前几步应给予最大的关注。
提前10-12步预测的主要目的是说明不同模型和预测方法的行为特征。在任何情况下，任何范围内获得的预测精度都可以使用置信区间限进行评估。本文的主要目的是说明一些有助于提高第[1]条所述指标的方法。
由于在前面的文章中已经介绍了求几个变量函数（用于生成指标）最小值的算法，因此我们不会在这里重复它们。为了简单起见，我们尽量减少理论内容。
nbsp；
1。初始指标
indicatores.mq5（见第[1]条）将用作起点。
要编译度量标准，我们需要使用指标。MQ5，火山灰。mqh和powell-smethod。同一目录中的MQH。这些文件可以在本文末尾的files2.zip文件中找到。
我们更新并定义了指数平滑模型在指数公式化过程中的方程，即线性衰减增长模型。
其中：
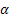-序列级平滑参数，[0,1]；
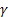——趋势平滑参数，[0,1]；
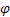衰减参数，[0,1]；
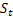—观察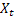
后，得到时间t计算的平滑序列水平。
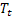——时间t计算的平滑加法趋势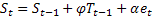；- 0-T；
的序列值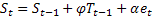 - 1——提前预测的步数；
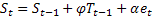- 2时间t阶跃预测；
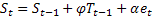- 3-时间t的一步进预测误差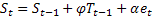，4。
索引的唯一输入参数是用于确定间隔长度的值，该值将用于优化模型参数并选择初始值（研究间隔）。在确定给定区间模型参数的最优值和所需计算后，将预先生成一步预测对应的预测、置信区间和相应的直线。对各新列的参数进行了相应的优化和预测。
为了更新指示器，我们将使用本文末尾files2.zip文件中的测试序列来评估更改结果。文件目录/dataset2中的文件包含已保存的欧元兑美元、美元兑瑞士法郎、美元兑日元报价和美元指数dxy。其中每一个都是为M1、H1和D1时间框架提供的。在文件中保存“open”值时，应在文件末尾保留最新值。每个文件包含1200个元素。
预测误差将通过计算“平均绝对百分比误差”（MAPE）系数来评估。
5
我们将12个测试序列的每个序列划分为50个重叠间隔，每个间隔包含80个元素，并计算每个元素的MAPE值。用这种方法得到的平均值将作为与比较指数相关的预测误差指数。采用同样的方法计算了两步和三步预测误差的MAPE值。这些平均估计数将进一步表示为：
- MAPE1-一步进预测误差的平均估计值；
- MAPE2-两步预测误差的平均提前估计值；
- MAPE3——提前三步预测误差的平均估计值；
- mape1-3-均值（mape1+mape2+mape3）/3。
在计算MAPE值时，绝对预测误差值除以每一步序列的当前值。为了避免在这个过程中被零除或得到负值，输入序列只需要取非零正值，在这种情况下。
初始指标的估计值如表1所示。
| MAP1 | MAP2 | MAP3 | MAPE1-3 | |
|---|---|---|---|---|
| 指示器 | 0.2099 | 0.2925 | 0.3564 | 0.2863 |
表1
。初始指标预测的估计误差
表1中显示的数据是使用errors_indicatores.mq5脚本（本文末尾的files2.zip文件）捕获的。要编译和运行此脚本，Cindicatores.mqh和Powell.mqh必须与Errors_Indicatores.mq5位于同一目录中，输入序列位于files/dataset2/目录中。
在获得预测误差的初始估计值后，我们现在可以继续升级研究中的指标。
2。优化准则
本文提出的“指数平滑法时间序列预测”中初始指标中的模型参数是通过进一步减小预测误差平方和来确定的。合理的做法是，预先优化的一步预测模型参数可能不会产生预先多步预测的最小误差。当然，最好将10-12步预测的误差降到最小，但在给定的研究序列范围内不可能获得满意的预测结果。
在实际中，在优化模型参数时，我们将采用一步、二步和三步预测误差的平方，首次对指标进行升级。在预测的前三个步骤中，平均误差可能会在一定程度上减少。
显然，这种初始指标的升级不涉及其主要结构的原理，而只是改变了参数优化准则。因此，我们不能期望预测的精度提高几倍，尽管前面两步和三步的预测误差应该减少一点。
为了比较预测结果，我们创建了一个与前面提到的带有修改的目标函数func的indicatores类相似的cmod1类。
初始Cindicatores类的函数：
double CIndicatorES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=0;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(Dlen*MathLog(k1*k2*k3*sse)); }
经过一些修改后，func功能的现状如下：
double CMod1::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,err,ae,pt,phi2,phi3,a; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95; // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 phi2=phi+phi*phi; phi3=phi2+phi*phi*phi; err=0; for(i=0;i<Dlen-2;i++) { e=Dat[i]-(s+phi*t); err+=e*e; a=Dat[i+1]-(s+phi2*t); err+=a*a; a=Dat[i+2]-(s+phi3*t); err+=a*a; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } e=Dat[Dlen-2]-(s+phi*t); err+=e*e; a=Dat[Dlen-1]-(s+phi2*t); err+=a*a; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; a=Dat[Dlen-1]-(s+phi*t); err+=a*a; return(k1*k2*k3*err); }
现在，在计算目标函数时，将使用前面一、二、三步预测误差的平方。
此外，基于这种开发类型的errors_mod1.mq5脚本允许估计预测错误，类似于前面提到的errors_indicatores.mq5脚本函数。cmod1.mqh和errors_mod1.mq5位于本文末尾的files2.zip文件中。
表2显示了初始版本和升级版本的估计预测错误。
| MAP1 | MAP2 | MAP3 | MAPE1-3 | |
|---|---|---|---|---|
| 指示器 | 0.2099 | 0.2925 | 0.3564 | 0.2863 |
| MOD1 | 0.2144 | 0.2898 | 0.3486 | 0.2842 |
表
2。估计预测误差比较
可以看出，MAPE2和MAPE3的误差系数以及MAPE1-3的平均值确实略低于研究中的序列。所以我们保存了这个版本，并继续进一步修订我们的指标。
三。平滑过程中的参数调整
根据输入序列的当前值改变平滑参数的想法既不是新的，也不是原始的，其目的是调整平滑系数，以便在给定输入序列的特性改变时保持最佳状态。一些调整平滑系数的方法将在参考文献[2]、[3]中解释。
为了进一步提高指数，我们将使用平滑系数动态变化的模型。我们希望使用自适应指数平滑模型来提高指数预测的准确性。
不幸的是，如果模型被用于预测算法中，大多数自适应方法并不总能得到理想的结果。选择合适的自适应方法可能太繁琐和耗时，因此在这种情况下，我们将使用参考文献[4]中提供的研究结果，并使用第[5]条中提到的“指数平滑的平滑变换”（stes）。
由于该方法的本质已在指定的文章中明确说明，因此我们暂时不必忽略它，只需考虑自适应平滑系数的使用，直接进入模型方程（见指定文章的开头）。
6
7
8
9
现在我们可以看到平滑系数alpha的值将根据平方预测误差在算法的每个步骤中进行计算。B和G系数的值决定了预测误差对α值的影响。在所有其他方面，所用模型的方程式保持不变。有关使用STES的更多详细信息，请参见第[6]条。
在以前的版本中，我们必须确定整个给定序列的最佳α系数，但是现在有两个自适应系数b和g要优化，α值在平滑输入序列的过程中动态确定。
升级采用cmod2类的形式。重大变化（如前一项）主要与func功能有关，现状如下。
double CMod2::func(const double &p[]) { int i; double s,t,alp,gam,phi,sb,sg,k1,k2,e,err,ae,pt,phi2,phi3,a; s=p[0]; t=p[1]; gam=p[2]; phi=p[3]; sb=p[4]; sg=p[5]; k1=1; k2=1; if (gam>0.95){k1+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k1+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k2+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k2+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 phi2=phi+phi*phi; phi3=phi2+phi*phi*phi; err=0; for(i=0;i<Dlen-2;i++) { e=Dat[i]-(s+phi*t); err+=e*e; a=Dat[i+1]-(s+phi2*t); err+=a*a; a=Dat[i+2]-(s+phi3*t); err+=a*a; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } e=Dat[Dlen-2]-(s+phi*t); err+=e*e; a=Dat[Dlen-1]-(s+phi2*t); err+=a*a; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; a=Dat[Dlen-1]-(s+phi*t); err+=a*a; return(k1*k2*err); }
当这个函数被开发出来时，定义α系数值的方程也将被稍微修改。这样做是为了将最大和最小允许值分别限制在0.05和0.95。
为了像以前一样评估预测错误，将基于cmod2类编写错误mod2.mq5脚本。cmod2.mqh和errors_mod2.mq5位于本文末尾的files2.zip文件中。
脚本结果如表3所示。
| MAP1 | MAP2 | MAP3 | MAPE1-3 | |
|---|---|---|---|---|
| 指示器 | 0.2099 | 0.2925 | 0.3564 | 0.2863 |
| MOD1 | 0.2144 | 0.2898 | 0.3486 | 0.2842 |
| MOD2 | 0.2145 | 0.2832 | 0.3413 | 0.2797 |
表
3。预测误差估计的比较
如表3所示，使用自适应平滑系数通常可以进一步略微减少测试序列中的预测误差。因此，在两次升级之后，我们设法将误差系数mape1-3减少了大约2个百分点。
虽然升级结果并不明显，但我们仍然坚持将其作为最终版本，并将进一步的升级留在本文之外进行讨论。在下一步中尝试使用Box-Cox转换是很好的。变换方法主要用于使初始序列分布接近正态分布。
在这个例子中，转换方法可以用来转换初始序列，计算预测，并对预测进行反向转换。该方法采用换算系数法，其选择应以最小化结果预测误差为原则。有关在预测序列中使用Box-Kax转换的示例，请参阅文章[7]。
4。预测置信区间
根据所选指数平滑模型的分析公式[8]计算初始指标.mq5指数（前面提到）中的预测置信区间。在这个例子中所做的改变导致了研究中模型的改变。由于平滑系数是可变的，因此不适合用上述分析表达式来估计置信区间。
以前使用的分析表达式是基于预测误差为对称正态分布的假设，这也是改变置信区间评价方法的另一个原因。由于我们的序列类不能满足这些要求，预测误差的分布可能不正常或对称。
在估计初始指标的置信区间时，应从输入序列开始计算一步预测误差的方差，然后用解析式计算二步、三步和多步预测的方差，得到一步预测误差的方差。
为了避免分析公式的使用，可以采用一种简单的方法，即通过输入序列直接计算提前两步、三步和更多步的方差，提前一步计算方差。然而，该方法有一个明显的缺陷：在短输入序列中，置信区间估计会比较分散，在计算方差和均方误差时不允许去除对期望误差正态性的限制。
在使用非参数自助方法（重采样）的过程中，我们可以找到解决这一问题的方法。这一思想的核心非常简单：如果用随机（均匀）分布代替初始序列的采样，生成的伪序列的分布将与初始序列的分布相同。
假设我们有一个n个成员的输入序列，通过在[0，n-1]范围内生成一个均匀分布的伪随机序列，并在从初始数组中采样时将这些值作为索引，我们可以生成一个明显长于初始序列的伪序列。也就是说，生成序列的分布将与原始序列的分布相同（几乎相同）。
估计置信区间的自助过程如下：
- 根据模型的输入序列，确定了指数平滑模型的参数、系数和自适应系数的最优初始值，并对模型进行了修正。如前所述，采用鲍威尔搜索算法确定最优参数。
- 利用最优模型参数对初始序列进行自始至终的遍历，建立了一个由一步预测误差组成的数组。数组元素的数目将等于输入序列长度n。
- 减去误差数组中每个元素的平均值以调整误差。
- 在[0，n-1]范围内的索引由伪随机序列发生器生成，并用它们构造了一个9999个元素长度的伪错误序列（重采样后）。
- 通过将人工生成的错误数组中的值插入定义当前使用模型的公式中，可以创建一个包含9999个伪输入序列值的数组。换句话说，我们必须将输入序列值插入到模型方程中，并相应地计算预测误差，但现在我们正在进行反向计算。对于数组中的每个元素，必须插入一个错误值来计算输入值。得到了一个与输入序列分布相同的9999个元素数组，其长度足以直接估计预测置信区间。
然后，利用生成的足够长的序列估计置信区间。为此，我们将使用以下场景：如果生成的预测错误数组按升序排列，则索引为249和9749的单元格中的值对应于95%置信区间[10]的限值，该限值位于包含9999个值的数组中。
为了更准确地估计预测间隔，数组长度应该是奇数。在本例中，预测置信区间的极限值通过以下方式估计：
- 利用前文确定的最优模型参数所产生的序列，建立了一个9999个一步预测误差数组。
- 对创建的数组进行排序；
- 从已排序的错误数组中选择索引249和9749的值（表示95%置信区间的极限值）。
- 提前重复步骤1、2和3，完成两个、三个和更多步骤。
用这种方法估计置信区间既有优点也有缺点。
其优点之一是不需要假定预测误差分布的性质。这种误差不需要正态或对称分布。此外，如果无法从使用的模型中推导出分析公式，则可以使用该方法。
所需计算范围的明显扩大以及对所用伪随机序列发生器质量评估的依赖性，都可以视为缺点。
利用重采样和分位数评价置信区间的方法比较原始，必须在某些方面加以改进。然而，在这种情况下，由于置信区间仅用于视觉评估，因此上述方法提供的精度似乎足够。
nbsp；
5。索引
修订版
考虑到本文描述的升级，建立了forecastes.mq5索引。对于重采样，我们使用前文[11]中提到的伪随机序列生成器。标准Mathrand（）生成器生成的结果稍差，这可能是由于标准Mathrand（）生成器生成的值[032767]范围不够。
编译forecasts.mq5度量时，powell.mqh、cfores.mqh和rndxor128.mqh都在同一目录中。以上所有文档都在fore.zip文件中。
以下是forecasts.mq5度量的源代码。
//+------------------------------------------------------------------+ //| ForecastES.mq5 | //| Copyright 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg." #property link "https://www.mql5.com" #property version "1.02" #property description "Forecasting based on the exponential smoothing." #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "ConfUp" // Confidence interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCrimson #property indicator_style3 STYLE_DOT #property indicator_width3 1 #property indicator_label4 "ConfDn" // Confidence interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCrimson #property indicator_style4 STYLE_DOT #property indicator_width4 1 input int nHist=80; // History bars, nHist>=24 #include "CForeES.mqh" #include "RNDXor128.mqh" #define NFORE 12 #define NBOOT 9999 double Hist[],Fore[],Conf1[],Conf2[]; double Data[],Err[],BSDat[],Damp[NFORE],BSErr[NBOOT]; int NDat; CForeES Es; RNDXor128 Rnd; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { NDat=nHist; if(NDat<24)NDat=24; MqlRates rates[]; CopyRates(NULL,0,0,NDat,rates); // Load missing data ArrayResize(Data,NDat); ArrayResize(Err,NDat); ArrayResize(BSDat,NBOOT+NFORE); SetIndexBuffer(0,Hist,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,Fore,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFORE); SetIndexBuffer(2,Conf1,INDICATOR_DATA); // Confidence interval PlotIndexSetString(2,PLOT_LABEL,"ConfUp"); PlotIndexSetInteger(2,PLOT_SHIFT,NFORE); SetIndexBuffer(3,Conf2,INDICATOR_DATA); // Confidence interval PlotIndexSetString(3,PLOT_LABEL,"ConfDN"); PlotIndexSetInteger(3,PLOT_SHIFT,NFORE); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,j,k,start; double s,t,alp,gam,phi,sb,sg,e,f,a,a1,a2; if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar start=rates_total-NDat; //----------------------- PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE); for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data Es.CalcPar(Data); // Optimization of parameters s=Es.GetPar(0); t=Es.GetPar(1); gam=Es.GetPar(2); phi=Es.GetPar(3); sb=Es.GetPar(4); sg=Es.GetPar(5); //---- a=phi; Damp[0]=phi; for(j=1;j<NFORE;j++){a=a*phi; Damp[j]=Damp[j-1]+a;} // Phi table //---- f=s+phi*t; for(i=0;i<NDat;i++) // History { e=Data[i]-f; Err[i]=e; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); Hist[start+i]=f; // History } for(j=0;j<NFORE;j++)Fore[rates_total-NFORE+j]=s+Damp[j]*t; // Forecast //---- a=0; for(i=0;i<NDat;i++)a+=Err[i]; a/=NDat; for(i=0;i<NDat;i++)Err[i]-=a; // alignment of the array of errors //---- f=Es.GetPar(0)+phi*Es.GetPar(1); for(i=0;i<NBOOT+NFORE;i++) // Resampling { j=(int)(NDat*Rnd.Rand_01()); if(j>NDat-1)j=NDat-1; e=Err[j]; BSDat[i]=f+e; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=s+phi*t; } //---- for(j=0;j<NFORE;j++) // Prediction intervals { s=Es.GetPar(0); t=Es.GetPar(1); f=s+phi*t; for(i=0,k=0;i<NBOOT;i++,k++) { BSErr[i]=BSDat[i+j]-(s+Damp[j]*t); e=BSDat[i]-f; a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); } ArraySort(BSErr); Conf1[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[249]; Conf2[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[9749]; } return(rates_total); } //-----------------------------------------------------------------------------------
为了便于演示，指示器应尽可能以直线代码执行。在编写代码时，并不打算对其进行优化。
图1和图2显示了该指标在两种不同情况下的结果。
0
&图1。forecastes.mq5指标的第一个运行示例
1
图2。forecastes.mq5指示器的第二个运行示例
图2清楚地表明95%的置信区间是不对称的。这是因为输入序列包含大量的异常值（由于预测错误的不对称分布）。
网站www.mql4.com和www.mql5.com之前提供了外推指标。我们采用其中一个指标——ar_outlocator_of_price.mq5并设置其参数值，如图3所示，以将其结果与使用这些指标获得的结果进行比较。
2
图3。MQ5指数的ar_外推法_的设置
这两个指标的运行是在不同时间框架内对欧元兑美元和美元兑瑞士法郎的直观比较。从表面上看，在大多数情况下，这两个指标将保持相同的方向。然而，经过长时间的观察，其中一个指标可能会遇到严重的分歧。也就是说，mq5的ar_外推法总是生成具有断点的预测线。
图4显示了一个与“price.mq5”指标的ar_外推法_同时运行的forecasts.mq5示例。
3
图4。预测结果比较
图4中的橙色实线显示了由ouprice.mq5指数的ar_外推得出的预测。
nbsp；
总结
本文的结果总结如下：
- 介绍了指数平滑模型在时间序列预测中的应用。
- 提出了一种模型实现的编程方案。
- 让您快速了解最佳初始值和模型参数选择相关问题；
- 该算法可以用鲍威尔方法编程求出多变量函数的最小值。
- 提出了一种利用输入序列优化预测模型参数的规划方法。
- 给出了预测算法升级的几个简单实例。
- 本文简要介绍了一种用自救法和分位数评价法预测置信区间的方法。
- 预报员。建立了MQ5预测指标，包括本文描述的所有方法和算法。
- 提供与此主题相关的文章、杂志和书籍的链接。
至于预测的结果。MQ5指标，需要注意的是，在某些情况下，使用鲍威尔法的优化算法不能根据给定的精度确定目标函数的最小值。在这种情况下，将达到允许的最大迭代次数，并在日志中显示相关消息。然而，这种情况在指标代码中并没有得到任何处理，这可以用来说明本文所描述的算法。但是，如果应用程序要求很严格，则需要以某种方式监视和处理这些实例。
为了进一步发展和加强这一预测指标，建议在每个步骤中同时使用不同的预测模型，目的是利用阿克克信息论准则进一步选择其中一个模型。或者，如果使用多个基本相似的模型，则应计算预测结果的加权平均值。在这种情况下，可以根据每个模型的预测误差系数来选择加权系数。
预测时间序列涵盖了广泛的主题，但不幸的是，这些文章只简要介绍了一些相关的问题。希望这些出版物有助于吸引读者对这一领域的预测和今后的工作的关注。
参考文献
- “指数平滑时间序列预测”。
- 于。P. Lukashin。时间序列短期预测的自适应方法：教科书。-.：Finansy I Statistika，2003年。- 416 pp.
- S.V. Bulashev。交易员统计。-：Kompania Sputnik+，2003年。- 245 pp.
- Everette S.Gardner Jr.，《指数平滑：最新技术——第二部分》。2005年6月3日。
- James W.Taylor，平滑过渡指数平滑。《预测杂志》，2004年，第23卷，第385-394页。
- James W.Taylor，平滑过渡指数平滑的波动性预测。国际预测杂志，2004年，第20卷，273-286页。
- Alysha M de Livera，《采用修正指数平滑状态空间框架的自动预测》，2010年4月28日，澳大利亚维多利亚州莫纳什大学经济和商业统计系，3800。
- Rob J.Hyndman等人使用两类新的状态空间模型预测指数平滑的时间间隔。2003年1月30日。
- 分位数日志。2007年9月第3期。
- 网址：https://ru.wikipedia.org/wiki/
- “时间序列的主要特征分析”。
本文由MetaQuotes Software Corp.翻译自俄语原文
，网址为https://www.mql5.com/ru/articles/346。
MyFxtop迈投(www.myfxtop.com)-靠谱的外汇跟单社区，免费跟随高手做交易！
免责声明：本文系转载自网络，如有侵犯，请联系我们立即删除，另：本文仅代表作者个人观点，与迈投财经（www.myfxtop.cn）无关。其原创性以及文中陈述文字和内容未经本站证实，对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺，请读者仅作参考，并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权，非商业转载请注明出处。
