介绍
模糊集的数学原理和模糊逻辑本身可以追溯到1965年。它的发现之父是伯克利大学的Lutfie Zad教授,他在《信息与控制杂志》上发表的一篇文章中首次介绍了“模糊集”的概念。对于精确的科学,如数学,该工具可以引入任何人都可以使用的模糊性概念,并为在软计算的基础上解决问题提供了一种基本的新方法。这些创新在当时的应用,可以极大地促进解决各种问题的过程,建立专家系统,建立神经网络。
然而,模糊逻辑的实际应用远不止这些。事实上,这种数学工具已经演变成主要用于自动控制理论。这可以进一步联系到另一个新概念——模糊模型的出现,这是数学模型的一个特例。
1。模糊集与模糊逻辑理论的背后
在某些方面,LutfieldZad的新理论扩展了我们所熟悉的数学逻辑和集合理论的边界。数学逻辑只有处理严格形式数据的能力,而一个特定集合的对象成员由两个概念定义。因此,特征“成员”具有离散值,具有两个含义:
- “1”-如果对象属于集合;
- “0”-如果对象不属于集合。
在模糊几何理论中,Lutfield Zad从“隶属度”的离散概念出发,引入了一个新的特征“隶属度”,正如以前使用的特征“集”已被“模糊集”所取代一样。
1.1。基本特征和定义
定义1。模糊集![]() 是域上的集对
是域上的集对![]() ,其中
,其中![]() 表示模糊集的元素隶属度
表示模糊集的元素隶属度![]() 。
。
定义2。成员身份是一个范围[0,1]内的数字。隶属度越高,宇宙中与模糊集属性相对应的元素越多。因此,如果隶属度等于0,则给定元素与集合不对应;相反,如果隶属度等于1,则成为完全对应。这是两种边界情况,不需要为常规集调用其他选项。所有其他选项的存在是区分模糊集的关键。
定义3。The membership function is a function that can calculate the membership degree from a random element to a fuzzy set in the universe. 因此,成员函数的域应该在[0,1]之内。在大多数情况下,隶属函数是一个连续单调函数。
定义4。语义变量是一种变量,其值是结合自然语言或人工语言的词或词。模糊集尤其由语义变量组成。在定义模糊集时,模糊变量的数目和性质对于每个独立的任务都是主观的。
定义5。特征集是所有可能值的集合,它是语义变量的可接受性。
定义6。特征可以是属于特征集的任何元素。在模糊集理论中,模糊集的一个特点是由隶属函数构成。每个特征的成员函数都是非常独立的,并且通常是唯一的。这些函数可以用多种方式构造:直接时间、间接时间和相对时间。这些通常是基于成员函数的特性和来自该领域专家的经验证据。
例如:
让我们定义一个称为“年龄”的语义变量。根据定义,“年龄”是一个周期,是人类、动物和植物生长和进化的一步。这个变量的最小值是0,这意味着某人甚至还没有一岁。最多设置为80。根据人们的年龄,我们可以给他以下的评价:“新生儿”、“青年”、“中年”、“老年”、“老年”等等。这个清单可以容纳相当多的项目。这将是我们的语义变量特性集,它的元素将是特性。
下图显示了一个模糊变量“年龄”的示例,其中只设置了三个特征集:青年、中年和老年。每个功能都有自己的成员资格功能。
让我们更深入地了解一些人30岁时的情况,这与图中的垂直线(30,0)相对应。这一行将在以下几点通过所有三个成员资格函数:
- (30,0)-曲线“年龄30”和曲线“年龄”的交叉点。
- (30,0.29)-曲线“30岁”和曲线“中年”的交叉点。
- (30,0.027)-曲线“年龄30”和曲线“青年”的交叉点。
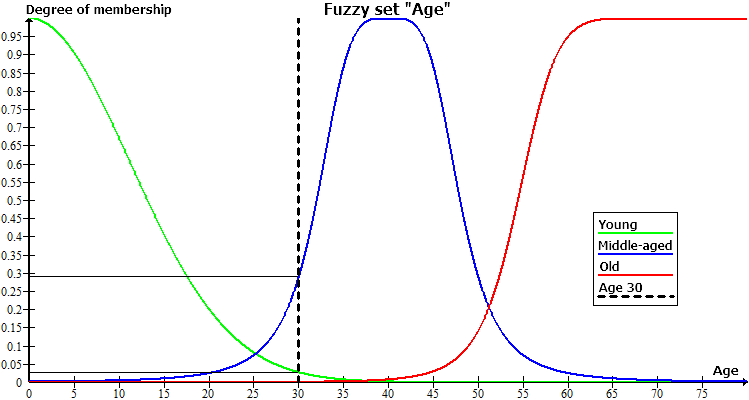
从这三点的坐标可以看出,一个30岁的人不能称为老年人,他接近青年和中年的特点,而第二个是占主导地位的。“中年”特征的成员数等于0.29,这是相当小的。事实上,另一个针对30岁儿童的专题“青年”将更合适。
定义7。去模糊化是将一个模糊集合转化为一个特定数字的过程。目前,已有20多种方法可供选择,其结果明显不同。请注意,到目前为止最好的结果是使用重心去模糊方法。
1.2。模糊逻辑
模糊逻辑-当语义变量被标记为真时,传统的亚里士多德逻辑被合成。模糊逻辑等价于经典逻辑,对定义的模糊集有自己的模糊逻辑运算。和普通集一样,模糊集的运算也一样,只是计算起来比较困难。我们还应该注意,多个模糊集的组合可以形成一个模糊集。
模糊逻辑的主要原理是古典逻辑的一部分,它尽可能地反映现实,具有较高的主观性,可能导致明显的计算误差。
模糊模型-基于模糊逻辑进行计算的数学模型。当研究课题形式化程度低、数学描述过于复杂或根本不清楚时,可以建立这些模型。这些模型的输出值(错误模型)的质量直接取决于构建模型的专家。减少错误的最佳选择是绘制一个更完整和详细的模型,该模型可以与一台学习机和一个大型训练集一起运行。
建模过程可分为三个主要阶段:
- 定义模型的输入和输出特性。
- 建立知识库。
- 选择一种模糊推理方法。
第一阶段直接影响到接下来的两个阶段,并决定模型的操作。知识库,有时是规则库,是一组模糊规则类型:“如果,那么”(如果,那么)。它定义了被检查对象的输入和输出之间的关系。系统中的规则数量没有限制,这也是由专家决定的。模糊规则的一般格式如下:
如果规则条件,则规则结论。
规则条件描述对象的当前状态,规则结论-此条件如何影响对象。条件和结论的一般观点不能被选择,因为它们是由模糊推理决定的。
系统中的每个规则都有其权重——这个特性定义了模型中每个规则的重要性。分配给每个规则的权重因子在[0,1]中。在许多模糊模型的例子中,这可以在相关文献中找到,没有指定的权重数据,但并不意味着它不存在。实际上,在这种情况下,规则库中每个规则的权重都固定为1。每个规则可以有两种特征和结论:
- 简单-包括模糊变量;
- 复杂性-包括几个模糊变量。
根据建立的知识库,确定了模型的模糊推理系统。模糊逻辑推理是模糊集与电流输入、知识库和模糊运算相适应的结论。两种模糊推理的主要类型是马达尼方法和观照方法。
1.3。马达尼型模糊推理
根据Madani类型算法,模糊推理的实现使用一个模糊知识库:
。
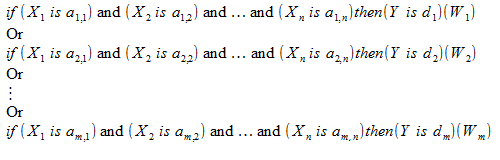
知识库中输入和输出变量的值由模糊集来设置。
此知识库也可以写成:
![]()
适用于:
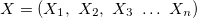 —输入变量矢量;
—输入变量矢量; 0—输出变量;
0—输出变量; 1—输入变量矢量j—th规则,j=0,1,2…m;
1—输入变量矢量j—th规则,j=0,1,2…m; 2—输出变量的矢量值;
2—输出变量的矢量值; 3重量j—th规则,j=0,1,2…M
3重量j—th规则,j=0,1,2…M
让我们介绍一个新的标记:![]() 4—模糊输入或输出变量的隶属函数V到模糊特征T.
4—模糊输入或输出变量的隶属函数V到模糊特征T.
。
模糊特征![]() 5输入向量隶属度的计算来自以下知识库:
5输入向量隶属度的计算来自以下知识库:
![]() 6-这一特征函数的结果来自知识库的J-规则。
6-这一特征函数的结果来自知识库的J-规则。
这里,![]() 7-S-Norm(T-Norm)操作实现多个或/和(或/和)逻辑操作。以下实现经常被使用:for或(或)operations-查找最大的,for和(和)operations-查找最小的。
7-S-Norm(T-Norm)操作实现多个或/和(或/和)逻辑操作。以下实现经常被使用:for或(或)operations-查找最大的,for和(和)operations-查找最小的。
在搜索了![]() 8对应的
8对应的![]() 9之后,我们得到了m个新的成员函数。它们一起形成一个新的模糊集,用
9之后,我们得到了m个新的成员函数。它们一起形成一个新的模糊集,用![]() 0和相应的输入向量
0和相应的输入向量![]() 1表示。
1表示。
![]() 2
2
这种模糊集的一个特点是其域是输出变量的特征集![]() 3。
3。
然后,需要以下内容:
- 截断成员函数
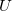 4位于级别
4位于级别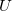 5。
5。 - 合并模糊集。
也就是说,利用模糊逻辑的特点,可以产生条件的意义和集合。建模有两种方法,意思是:找到最小或集合的乘积,聚合-找到最大或集合的算术和。
然后,我们得到结果模糊集,它的去模糊化将给我们准确的系统输出。
1.4。卡诺型模糊推理
根据Kano算法,模糊推理的实现使用模糊知识库:
![]() 6
6
官业知识库与马达尼知识库相似。除结论规则![]() 7外,它不是模糊特征定义,而是输入的线性函数:
7外,它不是模糊特征定义,而是输入的线性函数:
![]() 8
8
观叶知识库中的规则可以看作是确定性的开关,从一个线性规则“输入输出”到另一个规则,这也是线性的。子域的边界是模糊的,因此可以同时实现多个不同程度的线性规律。
此知识库也可以写成:
![]() 9
9
适用于:
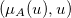 0—输入变量矢量。
0—输入变量矢量。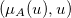 1—输出变量。
1—输出变量。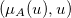 2-输入变量矢量j-th规则,j=0,1,2…M
2-输入变量矢量j-th规则,j=0,1,2…M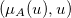 3——输出值线性函数中的自由特性系数j-th规则,j=0,1,2…M
3——输出值线性函数中的自由特性系数j-th规则,j=0,1,2…M- 当输出值的线性函数采用j-th规则时,其特征系数为
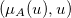 4-i-th,j=0,1,2…m,i=0,1,2…n.名词
4-i-th,j=0,1,2…m,i=0,1,2…n.名词 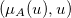 5加权j-th规则,j=0,1,2…M
5加权j-th规则,j=0,1,2…M
让我们介绍一个新的标记:![]() 6——模糊输入或输出变量的隶属函数V到模糊特征T.
6——模糊输入或输出变量的隶属函数V到模糊特征T.
。
模糊特征![]() 7输入向量隶属度的计算来自以下知识库:
7输入向量隶属度的计算来自以下知识库:
![]() 8-本征函数的结果来自知识库的j-次规则。
8-本征函数的结果来自知识库的j-次规则。
这里,![]() 9-s-norm(t-norm)操作实现多个或/和(或/和)逻辑操作。在官业型模糊推理中,经常使用以下三个三角范数的实现:或称为S范数,积为T范数。
9-s-norm(t-norm)操作实现多个或/和(或/和)逻辑操作。在官业型模糊推理中,经常使用以下三个三角范数的实现:或称为S范数,积为T范数。
在搜索了![]() 0中相应的
0中相应的![]() 1之后,我们得到了m个新的成员函数。它们一起形成一个新的模糊集,用
1之后,我们得到了m个新的成员函数。它们一起形成一个新的模糊集,用![]() 2和相应的输入向量
2和相应的输入向量![]() 3表示。
3表示。
![]() 4
4
注意,与Madani类型的输出相比,上述模糊集是一般模糊集的一阶。它是一组精确的数字。结果根据给定点![]() 6,将输出值
6,将输出值![]() 5定义为N维因子空间中的线性叠加。因此,模糊集
5定义为N维因子空间中的线性叠加。因此,模糊集![]() 7被去模糊化,计算平均重量或重量。
7被去模糊化,计算平均重量或重量。
2。模糊逻辑库
在实践中,创建和操作流程可能是一项困难的任务,即使只涉及一个非常简单的模糊模型。然而,有许多不同的软件工具和库可以大大简化它。作为一个例子,我们将研究来自Fuzzynet库的MQL5版本的测试脚本如何创建和操作两种模糊模型。
2.1。马达尼系统设计
第一个例子是Tips_sample_mamdani.mq5,来自Fuzzynet库的mql5版本。它实现了一个计算小费的模糊模型,即顾客根据其对服务和食品质量的评价来支付小费。该系统具有两个模糊逻辑输入和一个输出。知识库由三个规则组成,是一个马达尼逻辑输出系统。
输入参数是食品和服务的模糊变量,这两个变量的测量范围是0到10,这也是它们的最小值和最大值。变量“食物”包括两个特征:垃圾和美味。变量“服务”将由三个模糊特征组成:差、好和优。
在输出中,我们得到模糊变量“tip”。我们将定义票据金额的5%到30%范围内的小费,并为这个变量引入三个特征:吝啬、慷慨和慷慨。
系统的知识库包含三条规则:
- 如果(糟糕的服务)或(食物浪费),小费是小气的。
- 如果服务好,小费就正常了。
- 如果(优质服务)或(美味食物),小费要慷慨。
现在我们已经对系统有了一个大致的了解,我们将看看它的创建过程:
- 我们将包含文件mamdani fuzzy system.mqh,它来自fuzzynet:
的mql5版本库,include<;math/fuzzynet/mamdani fuzzy system.mqh>;此文件允许您创建和操作mamdani类型的系统。 - 现在我们可以创建一个空的mamdani模糊系统并将其填充:
mamdani fuzzy system*fstips=new mamdani fuzzy system(); - 我们将创建第一个输入变量service。将模糊变量创建为构造函数参数时,首先在一行中声明变量名,然后声明其最小值和最大值。
模糊变量*FVSERVICE=新的模糊变量(“服务”,0.0,10.0); - 我们为它添加了模糊特性。模糊特征构造器将字符串名称作为第一个参数,相应的成员函数作为第二个参数。
FV服务条款()。add(新模糊项(“差”,新三角形成员函数(-5.0,0.0,0.0,5.0));fvservice.terms()。add(新模糊项(“好”,新三角形成员函数(0.0,5.0,5.0,10.0));fvservice.terms();fvservice.terms()。加(新的模糊项()新的三角隶属函数(“优秀”),新的模糊三角隶属函数(5.0,新的隶属函数(5.0,10.0),新的三角隶属函数(10.0),新的三角隶属函数表示属函数,它是一个三角函数。 - 现有的模糊变量添加到我们的系统:
FSTIPS。输入()。添加(fvservice); - 同样,我们实现了第二个输入变量“food”,但是这个变量的特性将具有梯形的成员函数。6033 Fuzzy Variable * fvFood = new Fuzzy Variable (“food”, 0.0, 10.0); fvFood.Terms ().Add (new Fuzzy Term (“rancid”, new Trapezoid Membership Function (0.0, 0.0, 0.0, 1.0, 3.0)); fvFood.Fuzzy Terms (). 添加(新的模糊术语(“美味”,梯形成员函数(7.0,9.0,9.0,10.0,10.0),梯形成员函数梯形成员函数(7.0,9.0,10.0),新的梯形成员函数(7.0,10.0),新的梯形尖端infti()。添加(FvCouter);
- 由于系统具有Madani推理,因此其输入和输出值的确定方式相同。因此,以同样的方式,我们创建了类似的输出:
模糊变量*fvtips=新的模糊变量(“tips”,0.0,30.0);fvtips。Terms ().Add (new Fuzzy Term (“cheap”, new Triangular Membership Function (0.0, 5.0, 10.0)); fvTips. 术语()。添加(新的模糊项()函数(0.0,5.0,10.0,10.0));fvtips。术语()。添加(新模糊项()(新模糊三角项(“平均值”),成员函数成员函数(10.0,15.0,新成员函数(10.0,15.0())。添加(新的模糊术语)(“慷慨”,新的三角形成员函数(20.0,25.0,30.0);fstips。输出()。添加(FVTIP); - 创建模糊规则,作为系统知识库。要创建一个规则,它需要从对象调用方法parseRule来表示我们的系统,作为一个选项,给模糊规则一个简单的字符串表示:
MamDaniFuzzy Rule*Rule1=fstips。parserrule(“如果服务不好”或(食物变质),那么(小费很便宜)”;mamdanifuzzy rule*2=fstips。rule(“如果服务好)mamdani fuzzy rule*rule 3=fstips。parserrule(“如果(服务很好)或者(食物很美味)那么”);写模糊规则需要严格的输入,不允许使用非关键字。关键词是“if”、“then”、“is”、“and”、“or”、“not”、“little”、“some”、“very”、“extreme”。最后四个关键词是语义量词。此外,系统上可用的所有变量名、功能和函数都包含在关键字列表中。模糊特征或线性函数的重要性在增加,反之,语义量词的重要性在降低。下面的实现适用于语义量词:“轻微地”——用三次根代替条件结果。大大降低价值。
“有点”—用平方根代替条件的结果。降低价值。”非常”-将条件结果带到第二个级别。增加值。”极端的“—将有条件的结果带到第三层。最大值增加。 - 剩下的步骤是向系统中添加规则:
FSTIPS。规则()添加(规则1);fstips。规则()添加(规则2);fstips。规则()添加(规则3);
现在我们有了一个基于马达尼型模糊推理系统的现成的计算技巧模型。
2.2。非现场系统设计
作为一个例子,我们将使用一个脚本来测量车辆巡航控制系统的必要控制量。该脚本位于文件cruise_control_sample_sugeno.mq5中,来自于mql5版本的fuzzy net l库,并作为应用模糊模型解决自动控制问题的示例。
模糊逻辑主要用于自动控制系统(ACS)的等效一维任务。The settings of these targets can be described as follows: an object in the fixed point and time ![]() 8 state is “A”, and after a time frame
8 state is “A”, and after a time frame ![]() 9 it arrives at a condition “B”. 为了解决类似的任务,将整个时间段划分为
9 it arrives at a condition “B”. 为了解决类似的任务,将整个时间段划分为![]() 0个部分,已知时间片等于
0个部分,已知时间片等于![]() 1,然后自动控制系统在每个时间点的
1,然后自动控制系统在每个时间点的![]() 2进行管理,其中i=0、1、2……n.名词
2进行管理,其中i=0、1、2……n.名词
各种PID控制器可以很容易地处理这一任务,但它们的缺点是不能实现“平滑”控制。换句话说,如果你建立了一个基于PID控制器的巡航控制系统,系统将改变速度并调整到所需的速度,但在这个过程中可能会有跳跃和颠簸。从人的角度看,模糊控制器可以更顺利地实现,带来更好的舒适性。
显然,当输入误差和一阶导数误差发生时,模糊控制器的输出会要求速度的加速变化。错误是当前状态和预期值之间的偏差。换句话说,系统输入将接收以下信息:
- 车辆当前速度和巡航控制系统中设置的速度差;
- 差异减小(增加)的速度。
因此,“速度误差”的第一个输入参数在-20到20公里/小时之间,具有“慢”、“零”、“快”三个特点。所有三个功能都将具有三角形成员函数。第二个输入“速度误差点”在-5到5之间,而“速度误差”、“零”、“更快”的模糊特征运算也具有三角隶属度函数。
由于我们的模型与现场推理系统有关,“加速度”的输出值将不具有最大值和最小值,模糊特性将被输入变量的线性组合所代替,这也将被称为“零”、“更快”、“较慢”和“函数”。让我们描述所有四种线性组合。为此,我们将可变速度误差表示为![]() 3,速度误差点表示为
3,速度误差点表示为![]() 4,加速度表示为
4,加速度表示为![]() 5,得到如下方程:
5,得到如下方程:
- 零点:
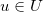 6;
6; - 更快:
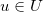 7;
7; - 慢:
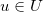 8;
8; - 功能:
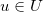 9。
9。
系统的知识库将包括九条规则:
- 如果(速度误差较慢),并且(速度误差点较慢),则加速更快。
- 如果(速度误差较慢),并且(速度误差点为零),则加速更快。
- 如果(速度误差较慢)和(速度误差点较快),则加速度为零。
- 如果(速度误差为零)和(速度误差点较慢),则加速更快。
- 如果(速度误差为零)和(速度误差点为零),加速度是一个函数。
- 如果(速度误差为零),并且(速度误差点更快),则加速较慢。
- 如果(速度误差更快)和(速度误差点较慢),则加速更快。
- 如果(速度误差较快),并且(速度误差点为零),则加速较慢。
- 如果(速度误差更快),并且(速度误差点更快),则加速较慢。
让我们描述一下系统创建的过程:
- 我们包括文件sugeno fuzzy system.mqh,它来自fuzzynet:
的mql5版本库include<;math/fuzzynet/sugeno fuzzy system.mqh>;此文件允许您创建非现场系统并对其进行操作。 - 现在我们可以创建一个空的网关系统并将其填充:
sugeno fuzzy system*fscruisecontrol=new sugeno fuzzy system(); - 在观音系统中创建输入变量的过程与在马达尼系统中相同。
636033我们将创建变量“速度错误”并将其添加到系统中:模糊变量*fvspeederror=新的fuzzy variable(“速度错误”,-20.0,20.0);fvspeederror.terms()。添加(新的模糊项(“较慢”,“新的三角形成员函数(-35.0,-20.0,-20.0,-5.0));fviderror。术语()。添加(模糊速度错误。术语()。加(模糊项(“新零”,新三角函数(“三角函数-15-三角函数-隶属度-0 0.0,15.0”)fvspeederror。术语()。添加(new fuzzyTerm(“更快”,新的三角形成员函数(5.0、20.0、35.0));我们将创建变量“speedErrorDot”并将其添加到系统中:fuzzyvariable*fvspeedErrorDot=new fuzzyvariable(“speedErrorDot”,-5.0、5.0、5.0);fvspeedErrorDorDot。斯佩珀多术语()。添加(new fuzzyterm(“fuzzyterm”)(new fuzzyterm(“new fuzzyterm”)(slow fuzzyfunction(“triangle membershipfunction trislow-9.0,-5.0,-1.0)))fvspeederrordot。术语()。添加(新的模糊项(“零”,新的三角形成员函数(-4.0,-0.0,4.0));fvspeedErrordot。术语()。加(新模糊项(“更快”,新三角隶属函数(1.0,5.0,9.0));
- 我们将创建非现场模糊变量,这将是系统的输出。创建模糊变量时,构造函数只接受其名称作为参数。线性函数可以添加到其中,但首先,这些函数需要确定,我们需要一个系数的双精度数组。
的线性函数是这样形成的:每个输入变量都是方程的一个未知数,系数取自一组系数。这样,数组中的系数必须与输入变量以相同的记录顺序放置。因此,对于第一个输入变量,系数下标应为0,对于第二个下标1,依此类推。因此,系数数组的长度必须大于一个单位,或等于输入变量的数目。如果长度相等,则自由特征的系数为零,否则该值将等于数组的最后一个元素。系统中有两个输入变量,因此系数数组的长度不应超过3。我们将声明所有四个数组,并根据它们的信息,根据上述描述形成函数,并将它们添加到非现场模糊变量中,然后将它们包含在系统中:
Sugenovariable*SVAccelerate=New Sugenovariable(“Accelerate”);Double Coeff1[3]=0.0,0.0 SVAccelerate。函数()。添加(fscruisecontrol.createSugenoFunction.(“零”,coeff1);double coefff2[3]==0.0,0.0,1.0 sVecceete.函数()添加(fscruisecontrol.createSugenoFunction(“更快”,coeff2));double coefff3[3]=0.0,0.0,-1.0;svAccelerate函数()。添加(fscruiseCreateControl sugenoControl控制函数(“较慢”,createControl control sugenoFunction(“较慢”,coefffffffffffff3));double coefff2]=[[2]]=-4-coefffcoefffcoefff4]]-0.04 0.0 svAccelerate。函数()。添加(fscruisecontrol.createsugenofunci)on(“func”,coeff4);fscruisecontrol。输出()。添加(SVAccelerate); - 与Madani系统不同,我们将创建九个规则:
Sugeno Fuzzy Rule*Rule 1=fsCruiseControl。parseRule(“如果(速度错误较慢)和(速度错误点较慢)则(加速较快)”;sugenozy rule*rule 2=fscruiseControl。parseRule(“如果(速度错误较慢)和(错误点为零),则(加速);sugenozy r rule*rule 3=fscruiseControl。parserrule(“如果(speederror较慢)和(speederror dot较快),则(accelerate为零)”;sugenofuzzyrule*规则4=fscruiseControl。规则*规则4=fscruiseControl。parserrule(“if(speederror为零)and(speedererror dot为慢)and(speederror dot为慢)and(acerate为快)”;sugenoffuzzy rule*sugenoffuzzy rule*5=sugenoffuzzy rule*5=fscruiserule(“speederror speedrule为零,ererror speedererror(speede)sugenoffuzzyrule*rule6=fscruisecontrol。parseRule(“如果(speedError为0)和(speedError dot为fast),则(accelerate error dot为fast),然后(accelerate为slow);sugenoFuzzyRule*rule7=fsCruiseControl。控制。parserrule(“if(eredror更快),speedErrordot更快”)speelerater rule(“sugenofuzzyrule*rule*rule*rule*rule 7=fscruiseControl”。parseRule(“如果(eredror更快),speedErrordot是speedErrordot,那么speeddor speed dot更快(accelerateRule 8=fs cruiseControl.parseRule(“如果(速度错误更快)”和(速度错误dot为零),那么(accelerate更慢);sugeno fuzzy rule*rule 9=fscruiseControl.parseRule(“如果(速度错误更快)”和(速度错误dot为fas)ter)然后(加速较慢)”; - 我们将它们添加到我们的系统中:A606033 ScruiseControl。规则()规则()添加(规则1);fscruisecontrol。规则()添加(规则2);fscruCruiseControl。规则()添加(规则3);fscruCruiseControl。规则()添加(规则3);fscruCruiseControl。规则()添加(规则4);fscrucruseControl。规则()规则()规则()添加(规则5);fscrucrucrucrucrucrucrucruCruiseControl。规则控制。规则()规则()。rurururururururules()。rurururururururules()。Ruruo L.规则()。添加(规则9);
2.3。马达尼型和官业型系统的计算
模糊变量及其值应发送到模糊系统的输入端。如上所述,模糊变量从其特征集中获取值。因此,系统的计算结果将取决于应用于相应模糊输入变量的特征值隶属度函数。然而,在大多数情况下,模糊度变量仅由发送到系统输入端的简单值形成,其目的是从输出端获得相同的精度。在这种情况下,证明了模糊特征没有被显式地表述,其隶属函数被表示为一个常数隶属函数。在这种特殊情况下,采用Fuzzynet库设计的系统进行操作。
需要将哪些内容发送到系统输入,我们将从其结果中获得什么形式的信息?
在模糊系统中,输入变量的数量没有限制。每个条目必须收集一些值。因此,我们需要有每个输入保存的值列表。这个列表的元素应该是一个包含两个字段的复杂对象:第一个字段-模糊变量和第二个字段-双精度数字类型。在文件字典中。mqh从mql5库fuzzynet中,类字典_obj_double已实现以创建此对象。
我们将为我们的Madani系统建立一个输入列表:
CList *in=new CList; Dictionary_Obj_Double *p_od_Service=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_Food=new Dictionary_Obj_Double; p_od_Service.SetAll(fvService, Service); p_od_Food.SetAll(fvFood, Food); in.Add(p_od_Service); in.Add(p_od_Food);
这里的service和food是两个具有双精度的输入参数类。
在上面的例子中,madani和guanye系统都只有一个输出,通常与输入相同,但是它们的数量没有限制。输入和输出的结构没有区别。
马达尼系统的输出:
CList *result=new CList; Dictionary_Obj_Double *p_od_Tips=new Dictionary_Obj_Double;
现在,对于每个系统,我们将调用一个函数calculate,它接受一个参数、一个输入列表,并返回一个输出列表。根据该列表的下标0,得到系统输出值,表示为Dictionary_obj_double class对象。使用它的类方法key和value,我们可以分别得到变量及其值。
我们将计算madani系统并显示模糊输出变量fvtips接收的数字:
result=fsTips.Calculate(in); p_od_Tips=result.GetNodeAtIndex(0); Alert("小费, %: ",p_od_Tips.Value());
我们将对Kano系统进行同样的操作:
CList *in=new CList; Dictionary_Obj_Double *p_od_Error=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_ErrorDot=new Dictionary_Obj_Double; p_od_Error.SetAll(fvSpeedError,Speed_Error); p_od_ErrorDot.SetAll(fvSpeedErrorDot,Speed_ErrorDot); in.Add(p_od_Error); in.Add(p_od_ErrorDot); CList *result=new CList; Dictionary_Obj_Double *p_od_Accelerate=new Dictionary_Obj_Double; result=fsCruiseControl.Calculate(in); p_od_Accelerate=result.GetNodeAtIndex(0); Alert("加速, %: ",p_od_Accelerate.Value()*100);
结论
有关上述脚本和创建模糊模型的更多信息,请下载fuzzynet库的mql5或mql4版本。必须理解的是,即使在辅助图书馆的协助下,“主动”模糊模型的构建也是一项具有挑战性的任务。此外,每一个完成的模型都需要彻底的强制性检查和调整。
参考文献和链接列表
- https://www.bindichen.co.uk/post/ai/mamdani-fuzzy-model.html-madani模糊模型。
- https://www.bindichen.co.uk/post/ai/takagi-sugeno-fuzzy-model.html-guanye模糊模型。
- https://reference.wolfram.com/applications/fuzzy logic/exampulation notebook/5.html-模糊逻辑控制。
- https://plato.stanford.edu/entries/logic-fuzzy-模糊逻辑简介。
- Lutfie Zad。模糊集及其应用
本文由MetaQuotes Software Corp.翻译自俄语原文
,网址为https://www.mql5.com/ru/articles/1991。
MyFxtop迈投(www.myfxtop.com)-靠谱的外汇跟单社区,免费跟随高手做交易!
免责声明:本文系转载自网络,如有侵犯,请联系我们立即删除,另:本文仅代表作者个人观点,与迈投财经(www.myfxtop.cn)无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。

 MyFxTops邁投財經
MyFxTops邁投財經
