简介
上世纪 90 年代,人工神经网络研究人员得出了一个结论:有必要为那些缺少网络层固定拓扑特征的运算机制,开发一个新的类。也就是说,人工神经在特征空间内的数量和布置并不会事先指定,而是在学习此类模型的过程中、根据输入数据的特性来计算,独立调节也与其适应。
之所以有这种想法,就是因为出现了大量输入参数的压缩和向量量化受阻的实际问题,比如语音与图像识别、抽象范式的分类与识别等。
因为当时 自组织映射与 赫布型学习已为人所知(尤其是生成网络拓扑 – 即在神经元之间创建一系列连接,构成一个“框架”层 – 的算法),而且 ”软“竞争学习的方法亦已算出(在此类流程中,权重不仅适应”赢家“神经元,还适用其”近邻“神经元),合理的步骤是将上述方法结合起来,而这已由德国科学家 Bernd Fritzke 于 1995 年完成,从而创建了如今的流行算法 “生长型神经气”(GNG)。
此方法被证实非常成功,所以出现了一系列由其衍生的修改版本;其中之一就是监督式学习的改编适应版本 (Supervised-GNG)。据作者称:与径向基函数网络相比,S-GNG 因其在难以分类的输入空间领域中的优化拓扑能力,而显示出强大得多的数据分类效率。勿庸置疑,GNG 要优于 “K-means” 聚类。
值得注意的是,2001 年,Fritzke 在接受德国证券交易所 (Deutsche Bӧrse) 的工作邀请之后,结束了自己在鲁尔大学(德国波鸿)的科研生涯。本文中之所以选择他的算法作为基础,这也是一个原因。
1. 生长型神经气
GNG 是一种允许实施输入数据自适应 聚类的算法,也就是说,不仅将空间划分为群集,还会基于数据的特性确定其所需数量。
该算法只以两个神经元开始,不断变化它们的数量(多数情况下是增长),同时,利用竞争赫布型学习法,在神经元之间创建一系列最佳对应输入向量分布的连接。每个神经元都有一个累积所谓“局部误差”的内部变量。节点之间的连接则以一个名为 “age” (年龄)的变量为特征。
GNG 伪代码如下所示:
- 初始化:创建两个带权重向量(输入向量的分布允许)的节点,以及局部误差的零值;将其年龄设为 0 以连接节点。
- 向神经网络
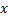 输入一个向量。
输入一个向量。 - 在最接近
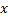 的地方找到
的地方找到 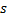 和
和 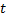 两个神经元,即带有权重向量
两个神经元,即带有权重向量 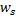 与
与 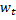 的节点,如此一来,
的节点,如此一来, 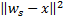 是所有节点中距离值最小、而
是所有节点中距离值最小、而 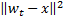 是第二小。
是第二小。 -
更新赢家神经元
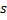 的局部误差,方法是将其添加到向量
的局部误差,方法是将其添加到向量 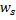 与
与 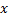 的平方距离:
的平方距离: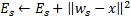
-
平移赢家神经元
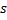 及其所有拓扑近邻点(即与该赢家有连接的所有神经元),方向是输入向量
及其所有拓扑近邻点(即与该赢家有连接的所有神经元),方向是输入向量 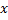 ,距离则等于部分
,距离则等于部分 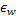 和整个
和整个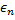 。
。

- 以 1 为步幅,增加从赢家
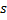 出来的所有连接的年龄。
出来的所有连接的年龄。 - 如果两个最佳神经元
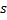 与
与 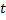 已连接,则将其连接的年龄设为零。否则就在它们之间创建一个连接。
已连接,则将其连接的年龄设为零。否则就在它们之间创建一个连接。 - 将年龄大于
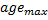 的连接移除。如果神经元中的这个结果没有更多的发散边缘,则亦将这些神经元移除。
的连接移除。如果神经元中的这个结果没有更多的发散边缘,则亦将这些神经元移除。 -
如果当前迭代的数量是
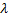 的倍数,且尚未达到网络的限制尺寸,则如下插入一个新的神经元
的倍数,且尚未达到网络的限制尺寸,则如下插入一个新的神经元 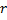 :
:- 确定带有一个最大局部误差的神经元
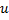 。
。 - 于近邻点中确定
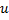 带有一个最大误差的神经元
带有一个最大误差的神经元 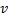 。
。 - 于
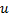 和
和 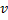 中间创建一个“居中”的节点
中间创建一个“居中”的节点 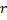 :
:
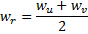
- 用
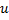 与
与 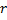 、
、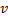 以及
以及 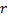 之间的边,替代
之间的边,替代 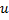 与
与 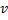 之间的边。
之间的边。 - 减少神经元
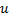 与
与 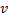 的误差,设置神经元
的误差,设置神经元 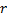 的误差值。
的误差值。
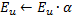
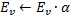
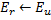
- 确定带有一个最大局部误差的神经元
-
利用分式
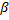 减少神经元
减少神经元 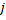 的所有误差。
的所有误差。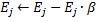
- 如果未能满足停止条件,则继续第 2 步。
我们来研究一下,生长型神经气如何适应输入空间的各种特性。
首先,请注意第 4 步赢家误差变量中的增长。这一流程表明,大多数赢的节点(即近邻点中出现最大数量输入信号的那些节点)都有最大的误差,因此,这些区域也是通过添加新节点进行“压缩”的主要备用区。
第 5 步中向输入向量方向的节点平移,意味着赢家在试图“平均化”位于其近邻点中各输入信号的仓位。这种情况下,最佳神经元会向信号方向少许“拉动”其近邻点(照例会选择 ![]() )。
)。
第 6-8 步中,我会讲到神经元相邻边缘的操作。原连接的老化和移除,是指网络的拓扑应最大程度地接近所谓的 狄洛尼三角剖分,即神经元的三角剖分(细分为三角形),其中,尤其是三角剖分中三角形的所有角的最小角都被最大化(避免“皮包骨型的”三角)。
简而言之,从层的最大熵、拓扑的意义上说,狄洛尼三角剖分对等于最“美”。要注意的是,要求拓扑结构不作为一个独立单元在其中,但在用于确定新节点(于第 8 步中插入)的位置时,它们始终位于某个边缘的中间。
步骤 p 是纠正层内所有神经元的误差变量。旨在确保网络“忘掉”原有的输入向量,从而更好地回应新的输入向量。由此,我们得到了使用生长型神经气以适应时间依赖型神经网络的可能性,即,输入信号的缓慢漂移分布。但是,这并未赋予其追踪输入特性中快速变化的能力(更多详情,请参阅下述讨论算法缺点的部分)。
可能我们要单独考虑停止条件。该算法因分析系统开发人员的想像力而天马行空。可能的选择有:检查测试设备相关的网络有效性、分析神经元平均误差的动态、限制网络的复杂程度等等。
出于说明考虑,我们使用最早的选项 – 因为本文的目的不仅是论述算法本身,还包括利用 MQL5 实现的可能性;我们会继续层的学习,直到输入用完(它们的数量自然是预定义的)。
2. 选择组织数据的方法
算法编程时,很明显,我们必然会面对存储所谓“集”的需求。我们会有两个集 – 一个神经元集和它们之间边缘的一个集。尽管两个结构都会在程序过程中演变(而且我们计划既添加项目又移除项目),但我们还是要为其提供机制。
当然,我们可以尝试使用对象的动态数组,但是那样我们就必须执行大量的数据复制移动操作,从而从根本上减慢程序的速度。使用带有指定属性抽象概念的更合适的选择就是程序图,而其最简单的版本则是链接表。
我会提醒读者们 链接表(图 1)的工作原理。基类的对象包含一个指向同一对象(作为成员之一)的指针,它允许无视内存中对象的物理顺序、将其合并成为线性结构。此外,还有一个 “carriage” 类,它会封装整个列表的所有流程,包括添加、插入和删除节点,搜索、对比和排序,以及其它必要的流程。

图 1. 线性链接表组织图示
MetaQuotes Software Corp. 的专家已经在标准库中实施了 CObject 类对象的链接表。相应的程序代码位于头文件 List.mqh 中,而该文件则位于 MetaTrader 5 标准交付包中的 MQL5/Include/Arrays。
我们不会从零开始,要相信 MetaQuotes 备受尊敬的程序人员的资质,将 CObject 与 CList 类作为我们数据结构的基础。这里我们会用到面向对象方法的一大支柱 – 继承机制。
3. 模型编程
首先,我们来定义“人工神经”概念的软件形式。
开发 OOP 应用的成规之一,就是始终从最常见的数据结构开始编程。就算是只为自己编写,也要如此。尤其是如果代码可能还要被其他程序人员使用的话,您要牢牢记住的是:将来的开发人员可能对程序逻辑的开发和修改有着不同的想法,而且,您也不可能事前知道哪些位置会被修改。
OOP 的原理意味着其他开发人员无需检查您的类,他们可以通过层级中适当位置的可用数据继承数据结构。因此,第一个编写的类要尽可能的抽象,随后再于较低层级添加细节,再逐步接近“罪恶的世界”。
说回到我们的问题,这意味着我们要从 CCustomNeuron 类的定义(“某种类型的神经元”)开始一个程序的编写,而且像所有人工神经一样,都会有一定数量的突触(输入权重)和输出值。它将具备初始化(为权重赋值)、计算其输出的信号值、甚至根据某指定值改变以适用其权重的能力。
我们很难更加抽象化了(考虑到我们是从一个最大泛化的 CObject 继承的类) – 所有神经元都必须具备执行指定动作的能力。
要描述数据,则创建一个头文件 Neurons.mqh,并将其放入 Include/GNG 文件夹。
//+------------------------------------------------------------------+ //| 用于引入神经元对象的基类 | //+------------------------------------------------------------------+ class CCustomNeuron:public CObject { protected: int m_synapses; double m_weights[]; public: double NET; CCustomNeuron(); ~CCustomNeuron(){}; void ZeroInit(int synapses); int Synapses(); void Init(double &weights[]); void Weights(double &weights[]); void AdaptWeights(double &delta[]); virtual void ProcessVector(double &in[]) {return;} virtual int Type() const { return(TYPE_CUSTOM_NEURON);} }; //+------------------------------------------------------------------+ //| 构造函数 | //+------------------------------------------------------------------+ void CCustomNeuron::CCustomNeuron() { m_synapses=0; NET=0; } //+------------------------------------------------------------------+ //| 返回神经元输入向量的维度 | //| 输入: 无 | //| 输出: 神经元的突触数量 | //+------------------------------------------------------------------+ int CCustomNeuron::Synapses() { return m_synapses; } //+------------------------------------------------------------------+ //| 使用0向量权重初始化神经元. | //| 输入: synapses - 突触数量 (输入权重) | //| 输出: 无 | //+------------------------------------------------------------------+ void CCustomNeuron::ZeroInit(int synapses) { if(synapses<1) return; m_synapses=synapses; ArrayResize(m_weights,m_synapses); ArrayInitialize(m_weights,0); NET=0; } //+------------------------------------------------------------------+ //| 使用一系列向量初始化神经元权重. | //| 输入: weights - 数据矢量 | //| 输出: 无 | //+------------------------------------------------------------------+ void CCustomNeuron::Init(double &weights[]) { if(ArraySize(weights)<1) return; m_synapses=ArraySize(weights); ArrayResize(m_weights,m_synapses); ArrayCopy(m_weights,weights); NET=0; } //+------------------------------------------------------------------+ //| 获得神经元权重的向量. | //| 输入: 无 | //| 输出: 权重 - 结果 | //+------------------------------------------------------------------+ void CCustomNeuron::Weights(double &weights[]) { ArrayResize(weights,m_synapses); ArrayCopy(weights,m_weights); } //+------------------------------------------------------------------+ //| 使用指定的数值修改神经元的权重 | //| 输入: delta - 校正向量 | //| 输出: 无 | //+------------------------------------------------------------------+ void CCustomNeuron::AdaptWeights(double &delta[]) { if(ArraySize(delta)!=m_synapses) return; for(int i=0;i<m_synapses;i++) m_weights[i]+=delta[i]; NET=0; }
此类中定义的函数都非常简单,这里就不再赘述。注意:我们已经定义了利用虚拟修饰符处理 ProcessVector(double &in[]) (此处的输出值像普通感知器一样计算)的输入数据函数。
这就意味着,如果按衍生类重新定义方法,则要根据运行时间的实际对象类动态地选择相应流程,如此会提高其灵活性,其中包括从用户交互的意义上来看,还会缩减编程的劳动力成本。
尽管我们似乎没做过什么链接表中神经元组织之类的事情,但事实上,当我们指出由 CObject 继承的新类的那一刻起,就已经在做了。所以,现在我们类的私有成员为 m_first_node、m_curr_node 和 m_last_node,皆为 “pointer at CObject” 类型,首先分别指出该表的当前与最后一个元素。巡览该表所需的所有函数,我们也都有。
现在,是时候通过 CGNGNeuron 类的定义,简单说说 GNG 层的神经元与其它同类的区别了:
//+------------------------------------------------------------------+ //| 一个 GNG 网络中的独立神经元 | //+------------------------------------------------------------------+ class CGNGNeuron:public CCustomNeuron { public: int uid; double E; double U; double error; CGNGNeuron(); virtual void ProcessVector(double &in[]); }; //+------------------------------------------------------------------+ //| 构造函数 | //+------------------------------------------------------------------+ CGNGNeuron::CGNGNeuron() { E=0; U=0; error=0; } //+------------------------------------------------------------------+ //| 计算神经元到输入向量的 "距离" | //| 输入: in - 数据向量 | //| 输出: 无 | //| 注意: 当前 "距离" 保存在 error 变量中, | //| "局部误差" 包含于另外的变量中, | //| 该变量叫做 E | //+------------------------------------------------------------------+ void CGNGNeuron::ProcessVector(double &in[]) { if(ArraySize(in)!=m_synapses) return; error=0; NET=0; for(int i=0;i<m_synapses;i++) { error+=(in[i]-m_weights[i])*(in[i]-m_weights[i]); } }
您可以看到,差异都已经摆在字段面前了:
- error – 从输入向量到神经元权重向量的当前距离平方,
- E – 一个累积局部误差和一个独特 ID 的变量,
- uid – 必须能够使我们通过组队连接进一步连接神经元(只是靠 CList 类中现有的简单索引并不够,因为我们还要添加和删除神经元,而这样做会导致编号混乱)。
ProcessVector(…) 函数已更改 – 现在它会计算 error 字段的值。
目前为止还不要注意 U 字段,它的意义稍后会在“算法修改”部分中讲到。
下一步是编写一个体现两个神经元之间连接的类。
//+------------------------------------------------------------------+ //| 定义两个神经元的连接 (边缘) 的类 | //+------------------------------------------------------------------+ class CGNGConnection:public CObject { public: int uid1; int uid2; int age; CGNGConnection(); virtual int Type() const { return(TYPE_GNG_CONNECTION);} }; //+------------------------------------------------------------------+ //| 构造函数 | //+------------------------------------------------------------------+ CGNGConnection::CGNGConnection() { age=0; }
这没什么难的 – 一条边有两个端(由标识符 uid1 与 uid2 指定的神经元)和初始设置为零的 age。
现在我们要使用链接表的 “carriages” 类,其中包含实施 GNG 算法的可能性。
首先从 CList 继承一个神经元列表类:
//+------------------------------------------------------------------+ //| 神经元链表 | //+------------------------------------------------------------------+ class CGNGNeuronList:public CList { public: //--- 构造函数 CGNGNeuronList() {MathSrand(TimeLocal());} CGNGNeuron *Append(); void Init(double &v1[],double &v2[]); CGNGNeuron *Find(int uid); void FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner); }; //+------------------------------------------------------------------+ //| 在列表末尾增加一个 "空白" 神经元 | //| 输入: 无 | //| 输出: 新神经元指针 | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGNeuron; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGNeuron; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; while(true) { int rnd=MathRand(); if(!CheckPointer(Find(rnd))) { ((CGNGNeuron *)m_curr_node).uid=rnd; break; } } //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| 根据向量的权重创建两个神经元 | //| 再用于初始化列表 | //| 输入: v1,v2 - 权重向量 | //| 输出: 无 | //+------------------------------------------------------------------+ void CGNGNeuronList::Init(double &v1[],double &v2[]) { Clear(); Append(); ((CGNGNeuron *)m_curr_node).Init(v1); Append(); ((CGNGNeuron *)m_curr_node).Init(v2); } //+------------------------------------------------------------------+ //| 根据 uid 搜索神经元 | //| 输入: uid - 神经元的唯一ID | //| 输出: 如果成功返回神经元指针, 否则返回 NULL | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Find(int uid) { if(!GetFirstNode()) return(NULL); do { if(((CGNGNeuron *)m_curr_node).uid==uid) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| 根据最小当前误差搜索两个 "最好的" 神经元 | //| 输入: 无 | //| 输出: Winner - 最 "接近" 输入向量的神经元 | //| SecondWinner - 第二 "接近" 的神经元 | //+------------------------------------------------------------------+ void CGNGNeuronList::FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) { double err_min=0; Winner=NULL; if(!CheckPointer(GetFirstNode())) return; do { if(!CheckPointer(Winner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min= ((CGNGNeuron *)m_curr_node).error; Winner = m_curr_node; } } while(CheckPointer(GetNextNode())); err_min=0; SecondWinner=NULL; GetFirstNode(); do { if(m_curr_node!=Winner) if(!CheckPointer(SecondWinner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min=((CGNGNeuron *)m_curr_node).error; SecondWinner=m_curr_node; } } while(CheckPointer(GetNextNode())); m_curr_node=Winner; }
在 constructor 类中,会有一个伪随机号码生成器被初始化:它会被用于分配列表独特标识符的各个元素。
我们来明确类方法的意义:
- Append() 方法是 CList 类功能性的一个添加。调用它时,就会有一个节点附到列表末尾处,或者,如果列表是空的,则创建第一个节点。
- Init(double &v1[],double &v2[]) 函数会因 GNG 算法而出现。记住:网络的生长从两个神经元开始,这一鲜明特征对我们而言最为方便。函数主体中采用 ID m_curr_node、m_first_node、m_last_node 时,如果我们想要使用此类的功能,则有必要显式将其转换为 CGNGNeuron* 类型(指定的变量继承自 CList,所以它们表面上都指向 CObject)。
- Find(int uid) 函数,功能如其名称,根据神经元的 ID 进行搜索,并返回一个指向发现元素的指针,如果没找到,则返回 NULL。
- FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) – 也是算法的一部分。我们要在神经元列表中搜索一个赢家,以及按照与输入向量接近程序与其邻近的一个赢家,这就是我们使用此函数的目的。注意参数是以引用的方式传递给该函数,这样我们之后才能在此写入返回值(*& 是指“引用一个指针” – 这是一种正确的语法,而倒过来的 &* 则表示被禁用的“某引用的指针”:这种情况下,编译器会生成一个错误)。
下一个类是神经元之间的一个连接列表。
//+------------------------------------------------------------------+ //| 神经元之间连接的链表 | //+------------------------------------------------------------------+ class CGNGConnectionList:public CList { public: CGNGConnection *Append(); void Init(int uid1,int uid2); CGNGConnection *Find(int uid1,int uid2); CGNGConnection *FindFirstConnection(int uid); CGNGConnection *FindNextConnection(int uid); }; //+------------------------------------------------------------------+ //| 在列表末尾增加一个"空白"连接 | //| 输入: 无 | //| 输出: 新绑定的指针 | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGConnection; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGConnection; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| 创建一个连接以初始化列表 | //| 输入: uid1,uid2 - 用于连接的神经元ID | //| 输出: 无 | //+------------------------------------------------------------------+ void CGNGConnectionList::Init(int uid1,int uid2) { Append(); ((CGNGConnection *)m_first_node).uid1 = uid1; ((CGNGConnection *)m_first_node).uid2 = uid2; m_last_node = m_first_node; m_curr_node = m_first_node; m_curr_idx=0; } //+------------------------------------------------------------------+ //| 检查神经元之间是否有连接 | //| 输入: uid1,uid2 - 神经元的ID | //| 输出: 如果有连接返回连接的指针, 否则返回 NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Find(int uid1,int uid2) { if(!CheckPointer(GetFirstNode())) return(NULL); do { if((((CGNGConnection *)m_curr_node).uid1==uid1 && ((CGNGConnection *)m_curr_node).uid2==uid2) ||(((CGNGConnection *)m_curr_node).uid1==uid2 && ((CGNGConnection *)m_curr_node).uid2==uid1)) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| 搜索指定的神经元的拓扑结构邻居 | //| 搜索范围为从第一个神经元开始的列表 | //| 输入: uid - 神经元ID | //| 输出: 如有连接返回连接的指针, 否则返回 NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindFirstConnection(int uid) { if(!CheckPointer(GetFirstNode())) return(NULL); while(true) { if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; if(!CheckPointer(GetNextNode())) return(NULL); } return(m_curr_node); } //+------------------------------------------------------------------+ //| 搜索指定的神经元的拓扑结构邻居 | //| 搜索范围是从当前神经元开始的神经元列表 | //| 输入: uid - 神经元ID | //| 输出: 如果有连接返回连接的指针, 否则返回 NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindNextConnection(int uid) { if(!CheckPointer(GetCurrentNode())) return(NULL); while(true) { if(!CheckPointer(GetNextNode())) return(NULL); if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; } return(m_curr_node); }
已定义的类方法:
- Append().此方法的实施与上述类差不多,只是返回类型不同(遗憾的是,MQL5 中没有类模板,所以我们每次都要编写这些内容)。
- Init(int uid1,int uid2) – GNG 算法要求一开始就在此函数中执行一个连接的初始化。
- Find(int uid1,int uid2) 函数清楚明了。
- FindFirstConnection(int uid) 与 FindNextConnection(int uid) 方法之间的差别在于,前者是从列表的开头开始查找带有一个邻近点的连接,而后者却是从邻近当前的节点开始 (m_curr_node)。
数据结构的相关描述到此结束。现在开始执行我们自己算法的编程。
4. 算法的类
创建一个新的头文件 GNG.mqh,将其置入 Include/GNG 文件夹。
//+------------------------------------------------------------------+ //| GNG.mqh | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #include "Neurons.mqh" //+------------------------------------------------------------------+ //| 体现 GNG 算法的主类 | //+------------------------------------------------------------------+ class CGNGAlgorithm { public: //--- 神经元对象以及它们之间连接的链表 CGNGNeuronList *Neurons; CGNGConnectionList *Connections; //--- 算法的参数 int input_dimension; int iteration_number; int lambda; int age_max; double alpha; double beta; double eps_w; double eps_n; int max_nodes; CGNGAlgorithm(); ~CGNGAlgorithm(); virtual void Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes); virtual bool ProcessVector(double &in[],bool train=true); virtual bool StoppingCriterion(); }; //+------------------------------------------------------------------+ //| 构造函数 | //+------------------------------------------------------------------+ CGNGAlgorithm::CGNGAlgorithm(void) { Neurons=new CGNGNeuronList(); Connections=new CGNGConnectionList(); Neurons.FreeMode(true); Connections.FreeMode(true); } //+------------------------------------------------------------------+ //| 析构函数 | //+------------------------------------------------------------------+ CGNGAlgorithm::~CGNGAlgorithm(void) { delete Neurons; delete Connections; } //+------------------------------------------------------------------+ //| 使用输入数据的两个向量初始化算法 | //| 输入: v1,v2 - 输入的向量 | //| __lambda - 在有新神经元插入时 | //| 迭代的次数 | //| __age_max - 连接的最大时间 | //| __alpha, __beta - 用于容错 | //| __eps_w, __eps_n - 用于适应权重 | //| __max_nodes - 神经网络大小的限制 | //| 输出: 无 | //+------------------------------------------------------------------+ void CGNGAlgorithm::Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes) { iteration_number=0; input_dimension=__input_dimension; lambda=__lambda; age_max=__age_max; alpha= __alpha; beta = __beta; eps_w = __eps_w; eps_n = __eps_n; max_nodes=__max_nodes; Neurons.Init(v1,v2); CGNGNeuron *tmp; tmp=Neurons.GetFirstNode(); int uid1=tmp.uid; tmp=Neurons.GetLastNode(); int uid2=tmp.uid; Connections.Init(uid1,uid2); } //+------------------------------------------------------------------+ //| 算法的主函数 | //| 输入: in - 输入数据的向量 | //| train - 如果为true, 开始学习, 否则 | //| 只计算神经元的输入值 | //| 输出: 如果符合停止条件返回true, 否则返回 false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::ProcessVector(double &in[],bool train=true) { if(ArraySize(in)!=input_dimension) return(StoppingCriterion()); int i; CGNGNeuron *tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.ProcessVector(in); tmp=Neurons.GetNextNode(); } if(!train) return(false); iteration_number++; //--- 寻找最接近 in[] 的两个神经元, 也就是对于向量的两个节点 //--- Ws 和 Wt, ||Ws-in||^2 是最小的并且 ||Wt-in||^2 - //---是所有节点中的第二短的距离. //--- ||*|| 表示欧几里得模数 CGNGNeuron *Winner,*SecondWinner; Neurons.FindWinners(Winner,SecondWinner); //--- 更新胜者的局部误差 Winner.E+=Winner.error; //--- 转换胜者和它的拓扑学邻居 (也就是 //--- 连接胜者的所有神经元) 在输入向量的方向 //--- 上的距离等于eps_w 和 eps_n 的分数. double delta[],weights[]; Winner.Weights(weights); ArrayResize(delta,input_dimension); for(i=0;i<input_dimension;i++) delta[i]=eps_w*(in[i]-weights[i]); Winner.AdaptWeights(delta); //--- 把所有连接胜者的连接年龄加1. CGNGConnection *tmpc=Connections.FindFirstConnection(Winner.uid); while(CheckPointer(tmpc)) { if(tmpc.uid1==Winner.uid) tmp = Neurons.Find(tmpc.uid2); if(tmpc.uid2==Winner.uid) tmp = Neurons.Find(tmpc.uid1); tmp.Weights(weights); for(i=0;i<input_dimension;i++) delta[i]=eps_n*(in[i]-weights[i]); tmp.AdaptWeights(delta); tmpc.age++; tmpc=Connections.FindNextConnection(Winner.uid); } //--- 如果联系了两个最佳神经元, 重置连接年龄. //--- 否则在它们之间创建一个连接. tmpc=Connections.Find(Winner.uid,SecondWinner.uid); if(tmpc) tmpc.age=0; else { Connections.Append(); tmpc=Connections.GetLastNode(); tmpc.uid1 = Winner.uid; tmpc.uid2 = SecondWinner.uid; tmpc.age=0; } //--- 删除所有年龄大于 age_max 的连接. //--- 如果结果中的神经元没有到其他节点的连接 //--- 删除那些神经元. tmpc=Connections.GetFirstNode(); while(CheckPointer(tmpc)) { if(tmpc.age>age_max) { Connections.DeleteCurrent(); tmpc=Connections.GetCurrentNode(); } else tmpc=Connections.GetNextNode(); } tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { if(!Connections.FindFirstConnection(tmp.uid)) { Neurons.DeleteCurrent(); tmp=Neurons.GetCurrentNode(); } else tmp=Neurons.GetNextNode(); } //--- 如果当前迭代的次数是 lambda 的倍数, 并且网络 //--- 还没有被遍历, 根据以下规则创建一个新的神经元 CGNGNeuron *u,*v; if(iteration_number%lambda==0 && Neurons.Total()<max_nodes) { //--- 1.寻找具有最大局部误差的神经元 u . tmp=Neurons.GetFirstNode(); u=tmp; while(CheckPointer(tmp=Neurons.GetNextNode())) { if(tmp.E>u.E) u=tmp; } //--- 2.在神经元 u 的邻居中确定有最大局部误差的那个. tmpc=Connections.FindFirstConnection(u.uid); if(tmpc.uid1==u.uid) v=Neurons.Find(tmpc.uid2); else v=Neurons.Find(tmpc.uid1); while(CheckPointer(tmpc=Connections.FindNextConnection(u.uid))) { if(tmpc.uid1==u.uid) tmp=Neurons.Find(tmpc.uid2); else tmp=Neurons.Find(tmpc.uid1); if(tmp.E>v.E) v=tmp; } //--- 3.在神经元u和v"之间"创建一个节点. double wr[],wu[],wv[]; u.Weights(wu); v.Weights(wv); ArrayResize(wr,input_dimension); for(i=0;i<input_dimension;i++) wr[i]=(wu[i]+wv[i])/2; CGNGNeuron *r=Neurons.Append(); r.Init(wr); //--- 4.使用 u 和 r 以及 v 和 r 之间的连接替换u和v之间的连接 tmpc=Connections.Append(); tmpc.uid1=u.uid; tmpc.uid2=r.uid; tmpc=Connections.Append(); tmpc.uid1=v.uid; tmpc.uid2=r.uid; Connections.Find(u.uid,v.uid); Connections.DeleteCurrent(); //--- 5.减少神经元 u 和 v 的误差, 把 //--- 神经元 r 和 u 的误差设为相同. u.E*=alpha; v.E*=alpha; r.E = u.E; } //--- 把所有神经元的误差减少 beta 的分数 tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.E*=(1-beta); tmp=Neurons.GetNextNode(); } //--- 检查停止标准 return(StoppingCriterion()); } //+------------------------------------------------------------------+ //| 停止标准. 在这个版本的文件中不做 | //| 处理, 总是返回 false. | //| 输入: 无 | //| OUTPUT: 如果满足标准返回 true, 否则返回 false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::StoppingCriterion() { return(false); }
CGNGAlgorithm 类有两个重要字段 – 神经元链接表的指针 Neurons 以及它们之间的连接 Connections。它们会是我们神经网络结构的物理介质。其余字段都是从外部定义的算法的参数。
我要从辅助类方法中挑选出 Init(…),将外部参数传递至算法的一个实例,执行数据结构初始化,而我们之前议定的停止条件 StoppingCriterion() 却什么都不做,始终返回 false。
作为该算法主函数、处理指定数据向量的 ProcessVector(…) 并不包含任何细节:我们完成了数据的组织以及使用它们的方法,所以说到算法时,我们就只需要照章完成所有步骤就好了。它们在代码中的位置,则由相应的注释指出。
5. 实际使用
我们根据 MetaTrader 5 终端的真实数据,来演示一下该算法的使用。
我们这里的目的,并不是创建一个基于 GNG 的有效“EA 交易”(一篇文章里不太能够讲清楚),我们只想知道生长型神经气是如何运行的,也就是所谓的“实况”演示。
要美化渲染数据,创建一个沿着价格轴在 0-100 范围内变化的空白窗口。为此,我们采用一个“空白”指标 Dummy.mq5 (没有其它函数):
//+------------------------------------------------------------------+ //| Dummy.mq5 | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #property version "1.00" #property indicator_separate_window #property indicator_minimum 0 #property indicator_maximum 100 #property indicator_buffers 1 #property indicator_plots 1 //--- Label1 绘图 #property indicator_type1 DRAW_LINE #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- 指标缓冲区 double DummyBuffer[]; //+------------------------------------------------------------------+ //| 自定义指标初始化函数 | //+------------------------------------------------------------------+ int OnInit() { //--- 指标缓冲区映射 SetIndexBuffer(0,DummyBuffer,INDICATOR_DATA); IndicatorSetString(INDICATOR_SHORTNAME,"GNG_dummy"); //--- return(0); } //+------------------------------------------------------------------+ //| 自定义指标迭代函数 | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime& time[], const double& open[], const double& high[], const double& low[], const double& close[], const long& tick_volume[], const long& volume[], const int& spread[]) { //--- 空缓冲区 ArrayInitialize(DummyBuffer,EMPTY_VALUE); //--- 返回 prev_calculated 值用于下次调用 return(rates_total); } //+------------------------------------------------------------------+
在 MetaEditor 中创建一个名为 GNG.mq5 的脚本 – 它会在 Dummy 指标的窗口中显示网络。
外部参数 – 学习用数据向量的数量以及该算法的参数:
//--- 用于学习的输入向量数量 input int samples=1000; //--- 算法参数 input int lambda=20; input int age_max=15; input double alpha=0.5; input double beta=0.0005; input double eps_w=0.05; input double eps_n=0.0006; input int max_nodes=100;
声明全局变量:
//---全局变量 CGNGAlgorithm *GNGAlgorithm; int window; int rsi_handle; int input_dimension; int _samples; double RSI_buffer[]; datetime time[];
开始编写 OnStart() 函数。首先,我们找到必要的窗口:
void OnStart() { int i,j; int window=ChartWindowFind(0,"GNG_dummy");
针对输入数据,我们采用 RSI 指标的值 – 因为该指标的值都已标准化为 0 到 100 的范围,所以我们无需再执行预处理,很方便。
对于神经网络的输入向量,我们假设是两个 RSI 值的配对 (input_dimension=2) – 分别在当前柱与前一柱上(学名叫做“某时间序列于某个二维特征空间的浸入”)。平展图表上显示二维向量更方便一些。
所以,首先准备数据初始化并创建一个该算法对象的实例:
//--- 为了使 CopyBuffer() 正确工作, 向量的数量 //--- 必须小于柱数 _samples=samples+input_dimension+10; if(_samples>Bars(_Symbol,_Period)) _samples=Bars(_Symbol,_Period); //--- 为算法接收输入数据 rsi_handle=iRSI(NULL,0,8,PRICE_CLOSE); CopyBuffer(rsi_handle,0,1,_samples,RSI_buffer); //--- 返回用户定义值 _samples=_samples-input_dimension-10; //--- 记住前面100个柱的开启时间 CopyTime(_Symbol,_Period,0,100,time); //--- 创建一个算法实例并设置输入数据的大小 GNGAlgorithm=new CGNGAlgorithm; input_dimension=2; //--- 数据向量 double v[],v1[],v2[]; ArrayResize(v,input_dimension); ArrayResize(v1,input_dimension); ArrayResize(v2,input_dimension); for(i=0;i<input_dimension;i++) { v1[i] = RSI_buffer[i]; v2[i] = RSI_buffer[i+3]; }
现在是算法初始化:
//--- 初始化
GNGAlgorithm.Init(input_dimension,v1,v2,lambda,age_max,alpha,beta,eps_w,eps_n,max_nodes);
绘制一个矩形框和信息标签(以可视化呈现该算法处理了多少迭代,网络中有多少神经元有“生长”):
//-- 画一个长方形框和信息标签 ObjectCreate(0,"GNG_rect",OBJ_RECTANGLE,window,time[0],0,time[99],100); ObjectSetInteger(0,"GNG_rect",OBJPROP_BACK,true); ObjectSetInteger(0,"GNG_rect",OBJPROP_COLOR,DarkGray); ObjectSetInteger(0,"GNG_rect",OBJPROP_BGCOLOR,DarkGray); ObjectCreate(0,"Label_samples",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_samples",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_YDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: 2"); ObjectCreate(0,"Label_neurons",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_neurons",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_neurons",OBJPROP_YDISTANCE,25); ObjectSetInteger(0,"Label_neurons",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: 2");
在主循环中,准备一个向量,以供算法的输入在图表上方作为一个蓝点显示:
//--- 开始算法主循环 i=2 因为有两个已经使用了 for(i=2;i<_samples;i++) { //--- 填充数据向量 (为了更清楚, 样本之间隔 //--- 3个柱 - 它们之间相互关联会少些) for(j=0;j<input_dimension;j++) v[j]=RSI_buffer[i+j*3]; //--- 在图表上显示向量 ObjectCreate(0,"Sample_"+i,OBJ_ARROW,window,time[v[0]],v[1]); ObjectSetInteger(0,"Sample_"+i,OBJPROP_ARROWCODE,158); ObjectSetInteger(0,"Sample_"+i,OBJPROP_COLOR,Blue); ObjectSetInteger(0,"Sample_"+i,OBJPROP_BACK,true); //--- 改变信息标签 ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: "+string(i+1));
将此向量传递至该算法(仅一个函数 – 这就是面向对象方法的优势所在!):
//--- 把输入向量传入算法用于计算
GNGAlgorithm.ProcessVector(v);
从图表中移除原有神经元,并绘制新的神经元(红圈)和连接(黄色虚线),分别用石灰色和绿色来高亮赢家与次优神经元。
//--- 我们需要在图表中删除连接中的旧神经元然后绘出新的神经元 for(j=ObjectsTotal(0)-1;j>=0;j--) { string name=ObjectName(0,j); if(StringFind(name,"Neuron_")>=0) { ObjectDelete(0,name); } else if(StringFind(name,"Connection_")>=0) { ObjectDelete(0,name); } } double weights[]; CGNGNeuron *tmp,*W1,*W2; CGNGConnection *tmpc; GNGAlgorithm.Neurons.FindWinners(W1,W2); //--- 绘制神经元 tmp=GNGAlgorithm.Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.Weights(weights); ObjectCreate(0,"Neuron_"+tmp.uid,OBJ_ARROW,window,time[weights[0]],weights[1]); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_ARROWCODE,159); //--- 赢家颜色为石灰色, 次优 - 绿色, 其他 - 红色 if(tmp==W1) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Lime); else if(tmp==W2) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Green); else ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Red); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_BACK,false); tmp=GNGAlgorithm.Neurons.GetNextNode(); } ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: "+string(GNGAlgorithm.Neurons.Total())); //--- 绘制连接 tmpc=GNGAlgorithm.Connections.GetFirstNode(); while(CheckPointer(tmpc)) { int x1,x2,y1,y2; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid1); tmp.Weights(weights); x1=weights[0];y1=weights[1]; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid2); tmp.Weights(weights); x2=weights[0];y2=weights[1]; ObjectCreate(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJ_TREND,window,time[x1],y1,time[x2],y2); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_WIDTH,1); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_STYLE,STYLE_DOT); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_COLOR,Yellow); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_BACK,false); tmpc=GNGAlgorithm.Connections.GetNextNode(); } ChartRedraw(); } //--- 从内存中删除算法实例 delete GNGAlgorithm; //--- 清空图表前先暂停 while(!IsStopped()); //--- 从图表上删除所有绘图 ObjectsDeleteAll(0,window); }
编译代码,启动 Dummy 指标,再于同一个图表上运行 GNG 脚本。图表上会出现如下画面:
您看到了吧,这种算法真的有效:网格逐渐适应于试图根据蓝点的生长密度覆盖其空间的新进数据。
视频只是展示了学习过程的第一步(仅 1000 迭代,而真实的 GNG 学习所需的向量数量可能会高达几万),但却已经让我们对整个过程有了相当程度的了解。
6. 已知问题
我们已经说过,GNG 的主要问题在于不具备追踪那些带有快速变化特性的非静态序列的能力。输入信号的这种“跳跃式”分布,可能导致已经取得特定拓扑结构的大多数 GNG 层神经元,忽然发现自己出局了。
而且,因为输入信号未落于所属位置的区域范围内,神经元之间的连接年龄并未增长,所以,网络中“记忆”信号原有特性的“死掉”的那部分,就不再做什么有用的工作,而只是耗用计算资源(参见图 2)。
缓慢漂移分布情况下未观测到该副作用:如果漂移速度在权重适应中与神经元的“移动速度”差不多,则 GNG 能够追踪相关变化。

图 2. 生长型神经气对于“跳跃式”分布的反应
如果赋予算法输入一个非常高的新神经元(参数 λ)插入频率,则网络上可能会出现独立的非活动(死掉)节点 。
其值过低会导致网络开始追踪那些重现可能性非常小、且在统计学上无关紧要的输入信号的分布辐射。如有一个 GNG 神经元插入此位置,此后很长一段时间,它都几乎一定会保持非活动状态。
此外,据实证研究显示:尽管低插入值有助于在学习过程的开头迅速减少平均网络误差,但培训结果却为此指标打出了最差的分数:这样的一种网络群集数据较粗糙。
7. 算法的修改
“跳跃式”分布的问题可以通过某种特定方式修改算法来解决。被普遍接受的修改,就是引入所谓的神经效用系数(带效用系数的 GNG 或称 GNG-U)。这种情况下,伪代码的变动最小,如下所示:
- 对于每一个神经元
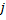 ,名为“效用系数”的变量
,名为“效用系数”的变量 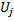 (即 CGNGNeuron 类字段列表中的 U 变量)都统一设置;
(即 CGNGNeuron 类字段列表中的 U 变量)都统一设置; -
在第 4 步、神经元赢家权重适合之后,我们会按照次优神经元与赢家神经元两者间的误差量来更改其效用系数:

实际上,这种添加的量,就是如果其中没有赢家,总网络误差会出现的变化(次优赢家就会成为赢家),即,神经元减少整体误差用途的实际特性。
-
神经元会在第 8 步中根据不同的原则予以移除:只移除带有最小效用值的节点,而且只在层中最大误差值超出其效用系数
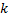 倍的情况下:
倍的情况下: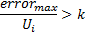
-
在第 9 步中添加一个新节点时,其效用系数是作为邻近神经元效用之间的算术平均值计算得出的:
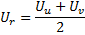
-
第 10 步中,所有神经元的效用系数都以同样方式、以误差变量的相同顺序下降:
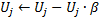
此处的常量 ![]() 是追踪非定常性能力的关键所在:如果其值过大,则不仅会导致真实的“小效用”被移除,还会移除其它非常有用的神经元;而如果值过小,又会导致移除量稀少,进而导致适应率降低。
是追踪非定常性能力的关键所在:如果其值过大,则不仅会导致真实的“小效用”被移除,还会移除其它非常有用的神经元;而如果值过小,又会导致移除量稀少,进而导致适应率降低。
GNG.mqh 文件中是将 GNG-U 算法作为由 CGNGAlgorithm 的一个衍生类描述的。读者朋友可自行追踪这些变化,试着用用这个算法。
总结
通过创建一个神经网络,我们温习了 MQL5 语言中内置面向对象编程的主要功能。很显然,如果没有此类机遇(借此感谢开发人员),要编写自动化交易的复杂程序可要困难得多。
至于我们分析过的算法,要注意的就是,一般来讲,它们都可以改进。尤其是,第一个要更新的,就是外部参数的数量。它们的数量庞大,这就意味着此类修改也不会少,其中一些参数会变成内部变量,且会基于输入数据的特性和算法的状态被选择。
对于那些学习神经信息学并将其运用到交易中去的人,本文作者希望他们好运!
本文译自 MetaQuotes Software Corp. 撰写的俄文原文
原文地址: https://www.mql5.com/ru/articles/163
(10.83 KB)
(181.3 KB)
MyFxtop迈投-靠谱的外汇跟单社区,免费跟随高手做交易!
免责声明:本文系转载自网络,如有侵犯,请联系我们立即删除,另:本文仅代表作者个人观点,与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。

 MyFxTops邁投財經
MyFxTops邁投財經
